
分析 (I)利用倍角公式、和差公式、正弦函数的单调性值域即可得出.
(II)利用三角函数求值、余弦定理、三角形面积计算公式即可得出.
解答 解:(Ⅰ)$f(x)=cosx(cosx+\sqrt{3}sinx)=cos{x^2}+\sqrt{3}sinxcosx$=$\frac{1+cos2x}{2}+\frac{{\sqrt{3}}}{2}sin2x$=$\frac{1}{2}+sin(2x+\frac{π}{6})$.
当$sin(2x+\frac{π}{6})=-1$时,f(x)取最小值为$-\frac{1}{2}$.
(Ⅱ)$f(C)=\frac{1}{2}+sin(2C+\frac{π}{6})=1$,∴$sin(2C+\frac{π}{6})=\frac{1}{2}$.
在△ABC中,∵C∈(0,π),$2C+\frac{π}{6}∈({\frac{π}{6},\frac{13π}{6}})$,∴$C=\frac{π}{3}$,
又c2=a2+b2-2abcosC,
(a+b)2-3ab=7.
∴ab=3.
∴${S_{△ABC}}=\frac{1}{2}absinC=\frac{{3\sqrt{3}}}{4}$.
点评 本题考查了倍角公式、和差公式、正弦函数的单调性值域、余弦定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
| A. | 甲、乙两人做游戏;甲、乙两人各写一个数字,若是同奇数或同偶数则甲胜,否则乙胜,这个游戏公平 | |
| B. | 做n次随机试验,事件A发生的频率就是事件A发生的概率 | |
| C. | 某地发行福利彩票,回报率为47%,某人花了100元买该福利彩票,一定会有47元的回报 | |
| D. | 实验:某人射击中靶或不中靶,这个试验是古典概型 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m⊆P | B. | m?P | C. | m∈P | D. | m∉P |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | [-1,1) | C. | [-1,0) | D. | (-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21号 | B. | 22号 | C. | 23号 | D. | 24号 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
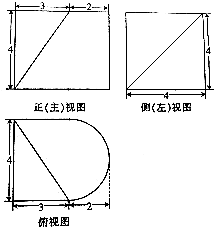
| A. | 44+2$\sqrt{34}$+8π | B. | 56+8π | C. | 44+2$\sqrt{34}$+12π | D. | 56+12π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com