
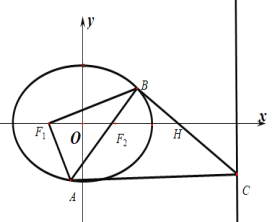
【题目】椭圆![]() 的焦点为
的焦点为![]() 和
和![]() ,过
,过![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,过
两点,过![]() 作与
作与![]() 轴垂直的直线
轴垂直的直线![]() ,又知点
,又知点![]() ,直线
,直线![]() 记为
记为![]() ,
,![]() 与
与![]() 交于点
交于点![]() .设
.设![]() ,已知当
,已知当![]() 时,
时,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求证:无论![]() 如何变化,点
如何变化,点![]() 的横坐标是定值,并求出这个定值.
的横坐标是定值,并求出这个定值.
【答案】(Ⅰ)![]() ;(Ⅱ)定值为3
;(Ⅱ)定值为3
【解析】
(Ⅰ)设椭圆的方程为![]()
![]() ,当
,当![]() 时,不妨设
时,不妨设![]() ,则
,则![]() ,由椭圆的定义得
,由椭圆的定义得![]() ,从而
,从而![]() ,可得点A在y轴上,不妨设
,可得点A在y轴上,不妨设![]() ,由
,由![]() 可得
可得![]() ,将B代入椭圆方程即可;
,将B代入椭圆方程即可;
(Ⅱ)设直线AB的方程为![]() ,
,![]() ,联立椭圆方程可得
,联立椭圆方程可得![]() ,进一步可得
,进一步可得![]() ,
,![]() ,利用点斜式可得BH的方程以及直线
,利用点斜式可得BH的方程以及直线![]() 的方程,解方程组即可.
的方程,解方程组即可.
(Ⅰ)设椭圆的方程为![]() ,其中
,其中![]() ,由已知,当
,由已知,当![]() 时,不妨设
时,不妨设![]() ,
,
则![]() ,又
,又![]() ,所以
,所以![]() ,由椭圆的定义得
,由椭圆的定义得![]() ,
,
从而![]() ,此时点A在y轴上,不妨设
,此时点A在y轴上,不妨设![]() ,
,
从而由已知条件![]() 可得
可得![]() ,解得
,解得![]() ,
,
故![]() ,代入椭圆方程,解得
,代入椭圆方程,解得![]() ,所以
,所以![]() ,
,
故所求椭圆方程为![]() .
.
(Ⅱ)设直线AB的方程为![]() ,
,![]() ,将
,将![]() 代入椭圆
代入椭圆
![]() 中,得
中,得![]() ,即
,即![]() ,
,
![]() ,所以
,所以![]() ,
,
由已知,![]() ,直线BH的斜率
,直线BH的斜率 ,
,
所以直线BH的方程为![]() ,而直线
,而直线![]() 的方程为
的方程为![]() ,代入
,代入![]() ,
,
解得![]() ,故点
,故点![]() 的横坐标是定值3.
的横坐标是定值3.


科目:高中数学 来源: 题型:
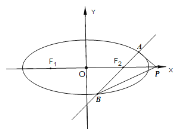
【题目】如图,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 与两焦点构成的三角形的周长为6,离心率为
与两焦点构成的三角形的周长为6,离心率为![]() ,
,
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,问在
两点,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?证明你的结论.
为定值?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B是椭圆C:![]() )的左右顶点,P点为椭圆C上一点,点P关于x轴的对称点为H,且
)的左右顶点,P点为椭圆C上一点,点P关于x轴的对称点为H,且![]()
(1)若椭圆C经过了圆![]() 的圆心,求椭圆C的标准方程;
的圆心,求椭圆C的标准方程;
(2)在(1)的条件下,抛物线D:![]() 的焦点F与点
的焦点F与点![]() 关于y轴上某点对称,且抛物线D与椭圆C在第四象限交于点Q,过点Q作直线与抛物线D有唯一公共点,求该直线与两坐标轴围成的三角形面积.
关于y轴上某点对称,且抛物线D与椭圆C在第四象限交于点Q,过点Q作直线与抛物线D有唯一公共点,求该直线与两坐标轴围成的三角形面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线C:y2=2px(p>0)的焦点为F,点P在C上,若PF⊥x轴,且△POF(O为坐标原点)的面积为1.
(1)求抛物线C的方程;
(2)若C上的两动点A,B(A,B在x轴异侧)满足![]() ,且|FA|+|FB|=|AB|+2,求|AB|的值.
,且|FA|+|FB|=|AB|+2,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校运动会男生组田径综合赛以选手三项运动的综合积分高低决定排名.具体积分规则如表1所示,某代表队四名男生的模拟成绩如表2.
表1 田径综合赛项目及积分规则
项目 | 积分规则 |
| 以 |
跳高 | 以 |
掷实心球 | 以 |
表2 某队模拟成绩明细
姓名 | 100米跑(秒) | 跳高(米) | 掷实心球(米) |
甲 |
|
|
|
乙 |
|
|
|
丙 |
|
|
|
丁 |
|
|
|
根据模拟成绩,该代表队应选派参赛的队员是:( )
A.甲B.乙C.丙D.丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在中美组织的暑假中学生交流会结束时,中方组织者将孙悟空、猪八戒、沙和尚、唐三藏、白龙马的彩色陶俑各一个送给来中国参观的美国中学生汤姆、杰克、索菲娅,每个人至少一个,且猪八戒的彩色陶俑不能送给索菲娅,则不同的送法种数为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:![]() 与曲线C:
与曲线C:![]() (
(![]() ,
,![]() )交于不同的两点A,B,O为坐标原点.
)交于不同的两点A,B,O为坐标原点.
(1)若![]() ,
,![]() ,求证:曲线C是一个圆;
,求证:曲线C是一个圆;
(2)若曲线C过![]() 、
、![]() ,是否存在一定点Q,使得
,是否存在一定点Q,使得![]() 为定值?若存在,求出定点Q和定值;若不存在,请说明理由.
为定值?若存在,求出定点Q和定值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com