
【题目】抛物线C:y2=2px(p>0)的焦点为F,点P在C上,若PF⊥x轴,且△POF(O为坐标原点)的面积为1.
(1)求抛物线C的方程;
(2)若C上的两动点A,B(A,B在x轴异侧)满足![]() ,且|FA|+|FB|=|AB|+2,求|AB|的值.
,且|FA|+|FB|=|AB|+2,求|AB|的值.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)先解出P点坐标,再表示△POF面积为![]() 1,解得p,进而得出抛物线方程.
1,解得p,进而得出抛物线方程.
(2)设直线AB方程为x=my+n,A(x1,y1),B(x2,y2),联立抛物线方程,消元x,可得含y的一元二次方程,由韦达定理可得y1+y2,y1y2,|AB|![]() ①,因为|FA|+|FB|=|AB|+2,得x1+x2=|AB|,2m2+2n=|AB|②由①②得2m2+2n
①,因为|FA|+|FB|=|AB|+2,得x1+x2=|AB|,2m2+2n=|AB|②由①②得2m2+2n![]() ,根据
,根据![]()
![]() 32,所以
32,所以![]() y1y2=32,n2﹣8n﹣128=0,进而得出答案.
y1y2=32,n2﹣8n﹣128=0,进而得出答案.
(1)由题知P点的横坐标为![]() ,代入抛物线方程得,y2=2p
,代入抛物线方程得,y2=2p![]() ,解得y=p或﹣p,
,解得y=p或﹣p,
所以P(![]() ,﹣p)或(
,﹣p)或(![]() ,p),△POF面积为
,p),△POF面积为![]() 1,解得p=2,
1,解得p=2,
所以抛物线C方程为y2=4x,S△OFP![]() .
.
(2)设直线AB方程为x=my+n,A(x1,y1),B(x2,y2)
联立抛物线方程得y2﹣2my﹣2n=0,y1+y2=2m,y1y2=﹣2n,
|AB|![]() ①
①
因为|FA|+|FB|=|AB|+2,所以x1+1+x2+1=|AB|+2,即x1+x2=|AB|,
my1+n+my2+n=|AB|,m(y1+y2)+2n=|AB|,2m2+2n=|AB|②
由①②得2m2+2n![]() ,化简得m2=n2﹣2n,
,化简得m2=n2﹣2n,
因为![]()
![]() 32,所以x1x2+y1y2=32,所以
32,所以x1x2+y1y2=32,所以![]() y1y2=32,
y1y2=32,
(y1y2)2+16y1y2﹣16×32=0,(﹣2n)2+16(﹣2n)﹣16×32=0,n2﹣8n﹣128=0,
解得n=﹣8(舍)或16,
所以|AB|=2m2+2n=2(n2﹣2n)+2n=2n2﹣2n=480.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|3x+2|.
(1)解不等式f(x)<4-|x-1|;
(2)已知m+n=1(m,n>0),若|x-a|-f(x)≤![]() (a>0)恒成立,求实数a的取值范围.
(a>0)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 垂直于
垂直于![]() 所在的平面
所在的平面![]() ,
,![]() 为
为![]() 的直径,
的直径,![]() 是弧
是弧![]() 上的一个动点(不与端点
上的一个动点(不与端点![]() 重合),
重合),![]() 为
为![]() 上一点,且
上一点,且![]() 是线段
是线段![]() 上的一个动点(不与端点
上的一个动点(不与端点![]() 重合).
重合).
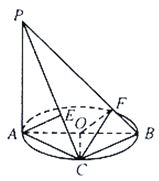
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 是弧
是弧![]() 的中点,
的中点,![]() 是锐角,且三棱锥
是锐角,且三棱锥![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的焦点为
的焦点为![]() 和
和![]() ,过
,过![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,过
两点,过![]() 作与
作与![]() 轴垂直的直线
轴垂直的直线![]() ,又知点
,又知点![]() ,直线
,直线![]() 记为
记为![]() ,
,![]() 与
与![]() 交于点
交于点![]() .设
.设![]() ,已知当
,已知当![]() 时,
时,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求证:无论![]() 如何变化,点
如何变化,点![]() 的横坐标是定值,并求出这个定值.
的横坐标是定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 点在
点在![]() 点左边)与直线
点左边)与直线![]() 交于点
交于点![]() .求
.求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有限数列![]() ,定义集合
,定义集合![]() 为数列
为数列![]() 的伴随集合.
的伴随集合.
(Ⅰ)已知有限数列![]() 和数列
和数列![]() .分别写出
.分别写出![]() 和
和![]() 的伴随集合;
的伴随集合;
(Ⅱ)已知有限等比数列![]() ,求
,求![]() 的伴随集合
的伴随集合![]() 中各元素之和
中各元素之和![]() ;
;
(Ⅲ)已知有限等差数列![]() ,判断
,判断![]() 是否能同时属于
是否能同时属于![]() 的伴随集合
的伴随集合![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a(lnx![]() 2)
2)![]() 1在定义域(0,2)内有两个极值点.
1在定义域(0,2)内有两个极值点.
(1)求实数a的取值范围;
(2)设x1和x2是f(x)的两个极值点,求证:lnx1+lnx2+lna![]() 0.
0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学就业部从该大学2018年毕业且已就业的大学本科生中随机抽取了100人进行了问卷调查,其中有一项是他们的薪酬,经调查统计,他们的月薪在3000元到10000元之间,根据统计数据得到如下频率分布直方图:
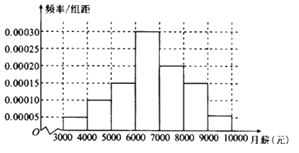
若月薪在区间![]() 的左侧,则认为该大学本科生属“就业不理想”的学生,学校将与本人联系,为其提供更好的指导意见.其中
的左侧,则认为该大学本科生属“就业不理想”的学生,学校将与本人联系,为其提供更好的指导意见.其中![]() ,
,![]() 分别是样本平均数和样本标准差,计算得
分别是样本平均数和样本标准差,计算得![]() (同一组中的数据用该组区间的中点值作代表)
(同一组中的数据用该组区间的中点值作代表)
(1)现该校2018届本科毕业生张静的月薪为3600元,判断张静是否属于“就业不理想”的学生?用样本估计总体,从该校2018届本科毕业生随机选取一人,属于“就业不理想”的概率?
(2)为感谢同学们对调查的支持配合,该校利用分层抽样的方法从样本的前3组中抽出6人,每人赠送一份礼品,并从这6人中再抽取2人,每人赠送新款某手机1部,求获赠手机的2人中恰有1人月薪不超过5000元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com