
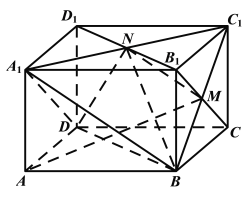
【题目】在四棱柱![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() .
.
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)求![]() 的长度;
的长度;
(Ⅲ)求直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]() 的长度等于
的长度等于![]() .(Ⅲ)
.(Ⅲ)![]()
【解析】
(Ⅰ)在以![]() 中,利用中位线定理证明
中,利用中位线定理证明![]() ,再由线面平行的判定定理得证;
,再由线面平行的判定定理得证;
(Ⅱ)由已知说明![]() ,
,![]() ,
,![]() 两两垂直,进而可建立空间直角坐标系,再分别表示点的坐标,即可表示
两两垂直,进而可建立空间直角坐标系,再分别表示点的坐标,即可表示![]() ,
,![]() 的坐标,由向量垂直的数量积为零构建方程求得答案;
的坐标,由向量垂直的数量积为零构建方程求得答案;
(Ⅲ)由数量积的坐标运算求夹角的余弦值.
(Ⅰ)证明:由已知,四棱柱![]() 中,四边形
中,四边形![]() 与四边形
与四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
所以![]() 中,
中,![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)因为![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() ,
,
又正方形![]() 中
中![]() ,所以以
,所以以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
设![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() ,
,
解得![]() ,所以
,所以![]() 的长度等于
的长度等于![]() .
.
(Ⅲ)由(Ⅱ)知![]() ,
,![]() ,
,
设直线![]() 与
与![]() 所成角为
所成角为![]() ,
,
所以![]() .
.
即直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】2020年席卷全球的新冠肺炎给世界人民带来了巨大的灾难,面对新冠肺炎,早发现、早诊断、早隔离、早治疗是有效防控疾病蔓延的重要举措之一.某社区对![]() 位居民是否患有新冠肺炎疾病进行筛查,先到社区医务室进行口拭子核酸检测,检测结果成阳性者,再到医院做进一步检查,己知随机一人其口拭子核酸检测结果成阳性的概率为
位居民是否患有新冠肺炎疾病进行筛查,先到社区医务室进行口拭子核酸检测,检测结果成阳性者,再到医院做进一步检查,己知随机一人其口拭子核酸检测结果成阳性的概率为![]() %,且每个人的口拭子核酸是否呈阳性相互独立.
%,且每个人的口拭子核酸是否呈阳性相互独立.
(1)假设该疾病患病的概率是![]() %,且患病者口拭子核酸呈阳性的概率为
%,且患病者口拭子核酸呈阳性的概率为![]() %,设这
%,设这![]() 位居民中有一位的口拭子核酸检测呈阳性,求该居民可以确诊为新冠肺炎患者的概率;
位居民中有一位的口拭子核酸检测呈阳性,求该居民可以确诊为新冠肺炎患者的概率;
(2)根据经验,口拭子核酸检测采用分组检测法可有效减少工作量,具体操作如下:将![]() 位居民分成若干组,先取每组居民的口拭子核酸混在一起进行检测,若结果显示阴性,则可断定本组居民没有患病,不必再检测;若结果显示阳性,则说明本组中至少有一位居民患病,需再逐个进行检测,现有两个分组方案:
位居民分成若干组,先取每组居民的口拭子核酸混在一起进行检测,若结果显示阴性,则可断定本组居民没有患病,不必再检测;若结果显示阳性,则说明本组中至少有一位居民患病,需再逐个进行检测,现有两个分组方案:
方案一:将![]() 位居民分成
位居民分成![]() 组,每组
组,每组![]() 人;
人;
方案二:将![]() 位居民分成
位居民分成![]() 组,每组
组,每组![]() 人;
人;
试分析哪一个方案的工作量更少?
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 与两焦点构成的三角形的周长为6,离心率为
与两焦点构成的三角形的周长为6,离心率为![]() ,
,
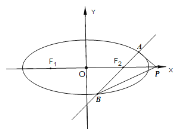
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,问在
两点,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?证明你的结论.
为定值?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,其图象关于直线
,其图象关于直线![]() 对称.给出下面四个结论:①将
对称.给出下面四个结论:①将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数图象关于原点对称;②点
个单位长度后得到函数图象关于原点对称;②点![]() 为
为![]() 图象的一个对称中心;③
图象的一个对称中心;③![]() ;④
;④![]() 在区间
在区间![]() 上单调递增.其中正确的结论为( )
上单调递增.其中正确的结论为( )
A.①②B.②③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B是椭圆C:![]() )的左右顶点,P点为椭圆C上一点,点P关于x轴的对称点为H,且
)的左右顶点,P点为椭圆C上一点,点P关于x轴的对称点为H,且![]()
(1)若椭圆C经过了圆![]() 的圆心,求椭圆C的标准方程;
的圆心,求椭圆C的标准方程;
(2)在(1)的条件下,抛物线D:![]() 的焦点F与点
的焦点F与点![]() 关于y轴上某点对称,且抛物线D与椭圆C在第四象限交于点Q,过点Q作直线与抛物线D有唯一公共点,求该直线与两坐标轴围成的三角形面积.
关于y轴上某点对称,且抛物线D与椭圆C在第四象限交于点Q,过点Q作直线与抛物线D有唯一公共点,求该直线与两坐标轴围成的三角形面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线C:y2=2px(p>0)的焦点为F,点P在C上,若PF⊥x轴,且△POF(O为坐标原点)的面积为1.
(1)求抛物线C的方程;
(2)若C上的两动点A,B(A,B在x轴异侧)满足![]() ,且|FA|+|FB|=|AB|+2,求|AB|的值.
,且|FA|+|FB|=|AB|+2,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(其中
,(其中![]() )的图象关于点
)的图象关于点![]() 成中心对称,且与点
成中心对称,且与点![]() 相邻的一个最低点为
相邻的一个最低点为![]() ,则对于下列判断:
,则对于下列判断:
①直线![]() 是函数
是函数![]() 图象的一条对称轴;
图象的一条对称轴;
②点![]() 是函数
是函数![]() 的一个对称中心;
的一个对称中心;
③函数![]() 与
与![]() 的图象的所有交点的横坐标之和为
的图象的所有交点的横坐标之和为![]() .
.
其中所有正确的判断是( )
A.①②B.①③C.②③D.②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com