
【题目】在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 点在
点在![]() 点左边)与直线
点左边)与直线![]() 交于点
交于点![]() .求
.求![]() 和
和![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程:
的参数方程: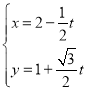 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆
轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)将直线![]() 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求圆![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,其图象关于直线
,其图象关于直线![]() 对称.给出下面四个结论:①将
对称.给出下面四个结论:①将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数图象关于原点对称;②点
个单位长度后得到函数图象关于原点对称;②点![]() 为
为![]() 图象的一个对称中心;③
图象的一个对称中心;③![]() ;④
;④![]() 在区间
在区间![]() 上单调递增.其中正确的结论为( )
上单调递增.其中正确的结论为( )
A.①②B.②③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机运动计步已成为一种时尚,某中学统计了该校教职工一天行走步数(单位:百步),绘制出如下频率分布直方图:
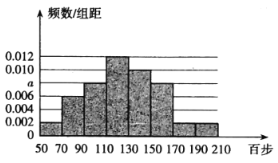
(Ⅰ)求直方图中![]() 的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
(Ⅱ)若该校有教职工175人,试估计一天行走步数不大于130百步的人数;
(Ⅲ)在(Ⅱ)的条件下该校从行走步数大于150百步的3组教职工中用分层抽样的方法选取6人参加远足活动,再从6人中选取2人担任领队,求这两人均来自区间![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线C:y2=2px(p>0)的焦点为F,点P在C上,若PF⊥x轴,且△POF(O为坐标原点)的面积为1.
(1)求抛物线C的方程;
(2)若C上的两动点A,B(A,B在x轴异侧)满足![]() ,且|FA|+|FB|=|AB|+2,求|AB|的值.
,且|FA|+|FB|=|AB|+2,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx-a![]() .
.
(1)若a=-1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若f(x)![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={(x,y)|(x﹣3﹣4cosq)2+(y﹣5﹣4sinq)2=4,θ∈R},B={(x,y)|3x+4y﹣19=0}.记集合P=A∩B,则集合P所表示的轨迹的长度为( )
A.8![]() B.8
B.8![]() C.8
C.8![]() D.8
D.8![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“未来肯定是非接触的,无感支付的方式将成为主流,这有助于降低交互门槛”.云从科技联合创始人姚志强告诉南方日报记者.相对于主流支付方式二维码支付,刷脸支付更加便利,以前出门一部手机解决所有,而现在连手机都不需要了,毕竟,手机支付还需要携带手机,打开二维码也需要时间和手机信号.刷脸支付将会替代手机,成为新的支付方式.某地从大型超市门口随机抽取50名顾客进行了调查,得到了如下列联表:
男性 | 女性 | 总计 | |
刷脸支付 | 18 | 25 | |
非刷脸支付 | 13 | ||
总计 | 50 |
(1)请将上面的列联表补充完整,并判断是否有95%的把握认为使用刷脸支付与性别有关?
(2)从参加调查且使用刷脸支付的顾客中随机抽取2人参加抽奖活动,抽奖活动规则如下:
“一等奖”中奖概率为0.25,奖品为10元购物券![]() 张(
张(![]() ,且
,且![]() ),“二等奖”中奖概率0.25,奖品为10元购物券两张,“三等奖”中奖概率0.5,奖品为10元购物券一张,每位顾客是否中奖相互独立,记参与抽奖的两位顾客中奖购物券金额总和为
),“二等奖”中奖概率0.25,奖品为10元购物券两张,“三等奖”中奖概率0.5,奖品为10元购物券一张,每位顾客是否中奖相互独立,记参与抽奖的两位顾客中奖购物券金额总和为![]() 元,若要使
元,若要使![]() 的均值不低于50元,求
的均值不低于50元,求![]() 的最小值.
的最小值.
附: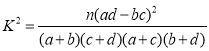 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.869 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆
是椭圆![]() 的右焦点,过点
的右焦点,过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,当直线
两点,当直线![]() 过
过![]() 的下顶点时,
的下顶点时,![]() 的斜率为
的斜率为![]() ,当直线
,当直线![]() 垂直于
垂直于![]() 的长轴时,
的长轴时,![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅲ)若直线![]() 上存在点
上存在点![]() 满足
满足![]() 成等比数列,且点
成等比数列,且点![]() 在椭圆外,证明:点
在椭圆外,证明:点![]() 在定直线上.
在定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com