
【题目】已知函数f(x)=a(lnx![]() 2)
2)![]() 1在定义域(0,2)内有两个极值点.
1在定义域(0,2)内有两个极值点.
(1)求实数a的取值范围;
(2)设x1和x2是f(x)的两个极值点,求证:lnx1+lnx2+lna![]() 0.
0.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)对函数进行求导可得![]() ,记g(x)=ex﹣1﹣ax,通过分类讨论得到函数单调性,分
,记g(x)=ex﹣1﹣ax,通过分类讨论得到函数单调性,分![]() 和
和![]() 两种情况进行讨论,即可得解;
两种情况进行讨论,即可得解;
(2)根据题意,将证明lnx1+lnx2+lna![]() 0,转化为证x1+x2
0,转化为证x1+x2![]() 2+lna,即证x1
2+lna,即证x1![]() 1﹣lnx2,结合(1)问转化成h(x)=lnx+e1﹣x
1﹣lnx2,结合(1)问转化成h(x)=lnx+e1﹣x![]() ,求导利用单调性即可证明.
,求导利用单调性即可证明.
(1)函数f(x)的定义域为(0,2),![]() ,记g(x)=ex﹣1﹣ax,则g′(x)=ex﹣1﹣a,
,记g(x)=ex﹣1﹣ax,则g′(x)=ex﹣1﹣a,
①当![]() 时,g′(x)
时,g′(x)![]() 0,
0,
故g(x)在(0,2)上单增,则g(x)至多有一个零点,不合题意;
②当![]() 时,令g′(x)=0得x=1+lna,
时,令g′(x)=0得x=1+lna,
(i)当1+lna<2且g(2)![]() 0,即
0,即![]() 时,
时,
g(x)在(0,1+lna)上单减,在(1+lna,2)上单增,
此时需g(x)min=g(1+lna)=﹣alna<0,解得a![]() 1,
1,
注意到g(0)![]() 0,
0,
故由零点存在性定理可知,g(x)在(0,1+lna)及(1+lna,2)上各有一个零点;
(ii)当1+lna![]() 2,即a
2,即a![]() e时,g(x)在(0,2)上单减,则g(x)至多有一个零点,不合题意;
e时,g(x)在(0,2)上单减,则g(x)至多有一个零点,不合题意;
综上,实数a的取值范围为![]() ;
;
(2)证明:不妨设0<x1<1+lna<x2<2,
由题意得,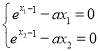 ,两边同时取自然对数得
,两边同时取自然对数得 ,
,
要证lnx1+lnx2+lna![]() 0,只需证x1+x2
0,只需证x1+x2![]() 2+lna,即证x1
2+lna,即证x1![]() 1﹣lnx2,
1﹣lnx2,
由上题可知,g(x)在(0,1+lna)上单减,则证明g(1﹣lnx2)![]() g(x1)=0即可,
g(x1)=0即可,
有![]() ,化简后即证明
,化简后即证明![]() 即可,
即可,
构造函数h(x)=lnx+e1﹣x,x∈(1+lna,2),则![]() ,注意到不等式ex﹣1
,注意到不等式ex﹣1![]() x(x
x(x![]() 0),
0),
则h′(x)![]() 0在(1+lna,2)恒成立,
0在(1+lna,2)恒成立,
即h(x![]() h(1+lna)
h(1+lna)![]() h(1)=1,故求证成立.
h(1)=1,故求证成立.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】2020年席卷全球的新冠肺炎给世界人民带来了巨大的灾难,面对新冠肺炎,早发现、早诊断、早隔离、早治疗是有效防控疾病蔓延的重要举措之一.某社区对![]() 位居民是否患有新冠肺炎疾病进行筛查,先到社区医务室进行口拭子核酸检测,检测结果成阳性者,再到医院做进一步检查,己知随机一人其口拭子核酸检测结果成阳性的概率为
位居民是否患有新冠肺炎疾病进行筛查,先到社区医务室进行口拭子核酸检测,检测结果成阳性者,再到医院做进一步检查,己知随机一人其口拭子核酸检测结果成阳性的概率为![]() %,且每个人的口拭子核酸是否呈阳性相互独立.
%,且每个人的口拭子核酸是否呈阳性相互独立.
(1)假设该疾病患病的概率是![]() %,且患病者口拭子核酸呈阳性的概率为
%,且患病者口拭子核酸呈阳性的概率为![]() %,设这
%,设这![]() 位居民中有一位的口拭子核酸检测呈阳性,求该居民可以确诊为新冠肺炎患者的概率;
位居民中有一位的口拭子核酸检测呈阳性,求该居民可以确诊为新冠肺炎患者的概率;
(2)根据经验,口拭子核酸检测采用分组检测法可有效减少工作量,具体操作如下:将![]() 位居民分成若干组,先取每组居民的口拭子核酸混在一起进行检测,若结果显示阴性,则可断定本组居民没有患病,不必再检测;若结果显示阳性,则说明本组中至少有一位居民患病,需再逐个进行检测,现有两个分组方案:
位居民分成若干组,先取每组居民的口拭子核酸混在一起进行检测,若结果显示阴性,则可断定本组居民没有患病,不必再检测;若结果显示阳性,则说明本组中至少有一位居民患病,需再逐个进行检测,现有两个分组方案:
方案一:将![]() 位居民分成
位居民分成![]() 组,每组
组,每组![]() 人;
人;
方案二:将![]() 位居民分成
位居民分成![]() 组,每组
组,每组![]() 人;
人;
试分析哪一个方案的工作量更少?
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线C:y2=2px(p>0)的焦点为F,点P在C上,若PF⊥x轴,且△POF(O为坐标原点)的面积为1.
(1)求抛物线C的方程;
(2)若C上的两动点A,B(A,B在x轴异侧)满足![]() ,且|FA|+|FB|=|AB|+2,求|AB|的值.
,且|FA|+|FB|=|AB|+2,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={(x,y)|(x﹣3﹣4cosq)2+(y﹣5﹣4sinq)2=4,θ∈R},B={(x,y)|3x+4y﹣19=0}.记集合P=A∩B,则集合P所表示的轨迹的长度为( )
A.8![]() B.8
B.8![]() C.8
C.8![]() D.8
D.8![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在中美组织的暑假中学生交流会结束时,中方组织者将孙悟空、猪八戒、沙和尚、唐三藏、白龙马的彩色陶俑各一个送给来中国参观的美国中学生汤姆、杰克、索菲娅,每个人至少一个,且猪八戒的彩色陶俑不能送给索菲娅,则不同的送法种数为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“未来肯定是非接触的,无感支付的方式将成为主流,这有助于降低交互门槛”.云从科技联合创始人姚志强告诉南方日报记者.相对于主流支付方式二维码支付,刷脸支付更加便利,以前出门一部手机解决所有,而现在连手机都不需要了,毕竟,手机支付还需要携带手机,打开二维码也需要时间和手机信号.刷脸支付将会替代手机,成为新的支付方式.某地从大型超市门口随机抽取50名顾客进行了调查,得到了如下列联表:
男性 | 女性 | 总计 | |
刷脸支付 | 18 | 25 | |
非刷脸支付 | 13 | ||
总计 | 50 |
(1)请将上面的列联表补充完整,并判断是否有95%的把握认为使用刷脸支付与性别有关?
(2)从参加调查且使用刷脸支付的顾客中随机抽取2人参加抽奖活动,抽奖活动规则如下:
“一等奖”中奖概率为0.25,奖品为10元购物券![]() 张(
张(![]() ,且
,且![]() ),“二等奖”中奖概率0.25,奖品为10元购物券两张,“三等奖”中奖概率0.5,奖品为10元购物券一张,每位顾客是否中奖相互独立,记参与抽奖的两位顾客中奖购物券金额总和为
),“二等奖”中奖概率0.25,奖品为10元购物券两张,“三等奖”中奖概率0.5,奖品为10元购物券一张,每位顾客是否中奖相互独立,记参与抽奖的两位顾客中奖购物券金额总和为![]() 元,若要使
元,若要使![]() 的均值不低于50元,求
的均值不低于50元,求![]() 的最小值.
的最小值.
附: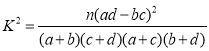 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.869 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(其中
,(其中![]() )的图象关于点
)的图象关于点![]() 成中心对称,且与点
成中心对称,且与点![]() 相邻的一个最低点为
相邻的一个最低点为![]() ,则对于下列判断:
,则对于下列判断:
①直线![]() 是函数
是函数![]() 图象的一条对称轴;
图象的一条对称轴;
②点![]() 是函数
是函数![]() 的一个对称中心;
的一个对称中心;
③函数![]() 与
与![]() 的图象的所有交点的横坐标之和为
的图象的所有交点的横坐标之和为![]() .
.
其中所有正确的判断是( )
A.①②B.①③C.②③D.②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月,教育部《关于在部分高校开展基础学科招生改革试点工作的意见》印发,自2020年起,在部分高校开展基础学科招生改革试点(也称“强基计划”).强基计划聚焦高端芯片与软件智能科技新材料先进制造和国家安全等关键领域以及国家人才紧缺的人文社会科学领域,选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生.新材料产业是重要的战略性新兴产业,下图是我国2011-2019年中国新材料产业市场规模及增长趋势图.其中柱状图表示新材料产业市场规模(单位:万亿元),折线图表示新材料产业市场规模年增长率(![]() ).
).
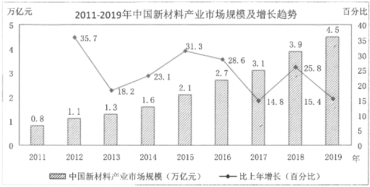
(1)求2015年至2019年这5年的新材料产业市场规模的平均数;
(2)从2012年至2019年中随机挑选一年,求该年新材料产业市场规模较上一年的年增加量不少于6000亿元的概率;
(3)由图判断,从哪年开始连续三年的新材料产业市场规模年增长率的方差最大.(结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com