
【题目】2020年1月,教育部《关于在部分高校开展基础学科招生改革试点工作的意见》印发,自2020年起,在部分高校开展基础学科招生改革试点(也称“强基计划”).强基计划聚焦高端芯片与软件智能科技新材料先进制造和国家安全等关键领域以及国家人才紧缺的人文社会科学领域,选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生.新材料产业是重要的战略性新兴产业,下图是我国2011-2019年中国新材料产业市场规模及增长趋势图.其中柱状图表示新材料产业市场规模(单位:万亿元),折线图表示新材料产业市场规模年增长率(![]() ).
).
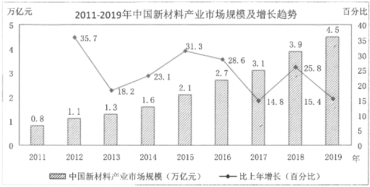
(1)求2015年至2019年这5年的新材料产业市场规模的平均数;
(2)从2012年至2019年中随机挑选一年,求该年新材料产业市场规模较上一年的年增加量不少于6000亿元的概率;
(3)由图判断,从哪年开始连续三年的新材料产业市场规模年增长率的方差最大.(结论不要求证明)
【答案】(1)3.26亿万元(2)![]() (3)从2012年开始连续三年的新材料产业市场规模年增长率的方差最大.
(3)从2012年开始连续三年的新材料产业市场规模年增长率的方差最大.
【解析】
(1)由柱状图表得出这5年的市场规模,运用公式求平均数即可;
(2)根据柱状图表算出从2012年起,每年新材料产业市场规模的增加值,利用古典概型算出概率;
(3)由折线图判断从2012年开始连续三年的新材料产业市场规模年增长率的方差最大.
(1)2015年至2019年这5年的新材料产业市场规模的平均数
![]() 万亿元;
万亿元;
(2)设![]() 表示事件“从2012年至2019年中随机挑选一年,读年新材料产业市场规模的增加值达到6000亿元”,从2012年起,每年新材料产业市场规模的增加值依次为:
表示事件“从2012年至2019年中随机挑选一年,读年新材料产业市场规模的增加值达到6000亿元”,从2012年起,每年新材料产业市场规模的增加值依次为:
3000,2000,3000,5000,6000,4000,8000,6000(单位:亿元),
所以![]() .
.
(3)从2012年开始连续三年的新材料产业市场规模年增长率的方差最大.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a(lnx![]() 2)
2)![]() 1在定义域(0,2)内有两个极值点.
1在定义域(0,2)内有两个极值点.
(1)求实数a的取值范围;
(2)设x1和x2是f(x)的两个极值点,求证:lnx1+lnx2+lna![]() 0.
0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学就业部从该大学2018年毕业且已就业的大学本科生中随机抽取了100人进行了问卷调查,其中有一项是他们的薪酬,经调查统计,他们的月薪在3000元到10000元之间,根据统计数据得到如下频率分布直方图:
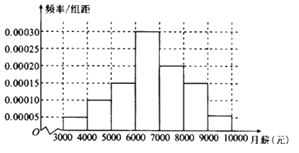
若月薪在区间![]() 的左侧,则认为该大学本科生属“就业不理想”的学生,学校将与本人联系,为其提供更好的指导意见.其中
的左侧,则认为该大学本科生属“就业不理想”的学生,学校将与本人联系,为其提供更好的指导意见.其中![]() ,
,![]() 分别是样本平均数和样本标准差,计算得
分别是样本平均数和样本标准差,计算得![]() (同一组中的数据用该组区间的中点值作代表)
(同一组中的数据用该组区间的中点值作代表)
(1)现该校2018届本科毕业生张静的月薪为3600元,判断张静是否属于“就业不理想”的学生?用样本估计总体,从该校2018届本科毕业生随机选取一人,属于“就业不理想”的概率?
(2)为感谢同学们对调查的支持配合,该校利用分层抽样的方法从样本的前3组中抽出6人,每人赠送一份礼品,并从这6人中再抽取2人,每人赠送新款某手机1部,求获赠手机的2人中恰有1人月薪不超过5000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,以x轴的非负半轴为极轴,建立极坐标系,已知直线l的参数方程为
中,以坐标原点为极点,以x轴的非负半轴为极轴,建立极坐标系,已知直线l的参数方程为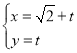 (t为参数),圆C的极坐标方程是
(t为参数),圆C的极坐标方程是![]() .
.
(1)求直线l与圆C的公共点个数;
(2)在平面直角坐标系中,圆C经过伸缩变换![]() 得到曲线
得到曲线![]() ,设
,设![]() 为曲线
为曲线![]() 上一点,求
上一点,求![]() 的最大值,并求相应点M的坐标.
的最大值,并求相应点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,平面ABC⊥平面BCD,△BAC与BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,BC=2,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成30°的角,则线段PA长的取值范围是( )
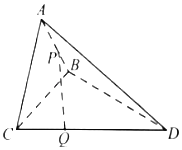
A.(0,![]() )B.[0,
)B.[0,![]() ]C.(
]C.(![]() ,
,![]() )D.(
)D.(![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自从新型冠状病毒爆发以来,全国范围内采取了积极的措施进行防控,并及时通报各项数据以便公众了解情况,做好防护.以下是湖南省2020年1月23日-31日这9天的新增确诊人数.
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
时间 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
新增确诊人数 | 15 | 19 | 26 | 31 | 43 | 78 | 56 | 55 | 57 |
经过医学研究,发现新型冠状病毒极易传染,一个病毒的携带者在病情发作之前通常有长达14天的潜伏期,这个期间如果不采取防护措施,则感染者与一位健康者接触时间超过15秒,就有可能传染病毒.
(1)将1月23日作为第1天,连续9天的时间作为变量x,每天新增确诊人数作为变量y,通过回归分析,得到模型![]() 用于对疫情进行分析.对上表的数据作初步处理,得到下面的一些统计量的值(部分数据已作近似处理):
用于对疫情进行分析.对上表的数据作初步处理,得到下面的一些统计量的值(部分数据已作近似处理):![]() ,
,![]() .根据相关数据,求该模型的回归方程(结果精确到0.1),并依据该模型预测第10天新增确诊人数.
.根据相关数据,求该模型的回归方程(结果精确到0.1),并依据该模型预测第10天新增确诊人数.
(2)如果一位新型冠状病毒的感染者传染给他人的概率为0.3,在一次12人的家庭聚餐中,只有一位感染者参加了聚餐,记余下的人员中被感染的人数为![]() ,求
,求![]() 最有可能(即概率最大)的值是多少.
最有可能(即概率最大)的值是多少.
附:对于一组数据![]() ,
,![]() …,
…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为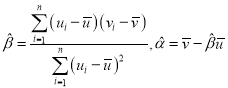 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,下述四个结论:
,下述四个结论:
①![]() 是偶函数;
是偶函数;
②![]() 的最小正周期为
的最小正周期为![]() ;
;
③![]() 的最小值为0;
的最小值为0;
④![]() 在
在![]() 上有3个零点
上有3个零点
其中所有正确结论的编号是( )
A.①②B.①②③C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某音乐院校举行“校园之星”评选活动,评委由本校全体学生组成,对![]() 两位选手,随机调查了
两位选手,随机调查了![]() 个学生的评分,得到下面的茎叶图:
个学生的评分,得到下面的茎叶图:
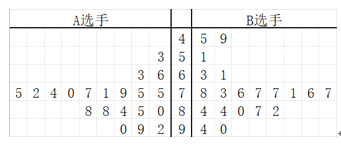
![]() 通过茎叶图比较
通过茎叶图比较![]() 两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
![]() 校方将会根据评分记过对参赛选手进行三向分流:
校方将会根据评分记过对参赛选手进行三向分流:
所得分数 | 低于 |
| 不低于 |
分流方向 | 淘汰出局 | 复赛待选 | 直接晋级 |
记事件![]() “
“![]() 获得的分流等级高于
获得的分流等级高于![]() ”,根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件
”,根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com