
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,以x轴的非负半轴为极轴,建立极坐标系,已知直线l的参数方程为
中,以坐标原点为极点,以x轴的非负半轴为极轴,建立极坐标系,已知直线l的参数方程为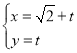 (t为参数),圆C的极坐标方程是
(t为参数),圆C的极坐标方程是![]() .
.
(1)求直线l与圆C的公共点个数;
(2)在平面直角坐标系中,圆C经过伸缩变换![]() 得到曲线
得到曲线![]() ,设
,设![]() 为曲线
为曲线![]() 上一点,求
上一点,求![]() 的最大值,并求相应点M的坐标.
的最大值,并求相应点M的坐标.
科目:高中数学 来源: 题型:
【题目】已知集合A={(x,y)|(x﹣3﹣4cosq)2+(y﹣5﹣4sinq)2=4,θ∈R},B={(x,y)|3x+4y﹣19=0}.记集合P=A∩B,则集合P所表示的轨迹的长度为( )
A.8![]() B.8
B.8![]() C.8
C.8![]() D.8
D.8![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆
是椭圆![]() 的右焦点,过点
的右焦点,过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,当直线
两点,当直线![]() 过
过![]() 的下顶点时,
的下顶点时,![]() 的斜率为
的斜率为![]() ,当直线
,当直线![]() 垂直于
垂直于![]() 的长轴时,
的长轴时,![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅲ)若直线![]() 上存在点
上存在点![]() 满足
满足![]() 成等比数列,且点
成等比数列,且点![]() 在椭圆外,证明:点
在椭圆外,证明:点![]() 在定直线上.
在定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定直线
到定直线![]() 的距离与到定点
的距离与到定点![]() 的距离之比为
的距离之比为![]() .
.
(1)求![]() 点的轨迹
点的轨迹![]() 的方程;
的方程;
(2)已知点![]() ,在
,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得曲线
,使得曲线![]() 上另有一点
上另有一点![]() ,满足
,满足![]() ,且
,且![]() ?若存在,求出所有符合条件的点
?若存在,求出所有符合条件的点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月,教育部《关于在部分高校开展基础学科招生改革试点工作的意见》印发,自2020年起,在部分高校开展基础学科招生改革试点(也称“强基计划”).强基计划聚焦高端芯片与软件智能科技新材料先进制造和国家安全等关键领域以及国家人才紧缺的人文社会科学领域,选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生.新材料产业是重要的战略性新兴产业,下图是我国2011-2019年中国新材料产业市场规模及增长趋势图.其中柱状图表示新材料产业市场规模(单位:万亿元),折线图表示新材料产业市场规模年增长率(![]() ).
).
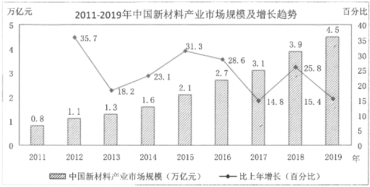
(1)求2015年至2019年这5年的新材料产业市场规模的平均数;
(2)从2012年至2019年中随机挑选一年,求该年新材料产业市场规模较上一年的年增加量不少于6000亿元的概率;
(3)由图判断,从哪年开始连续三年的新材料产业市场规模年增长率的方差最大.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活中人们常用“通五经贯六艺”形容一个人才识技艺过人,这里的“六艺”其实源于中国周朝的贵族教育体系,具体包括“礼、乐、射、御、书、数”.为弘扬中国传统文化,某校在周末学生业余兴趣活动中开展了“六艺”知识讲座,每艺安排一节,连排六节,则满足“数”必须排在前两节,“礼”和“乐”必须分开安排的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样检查,测得身高情况的统计图如下:
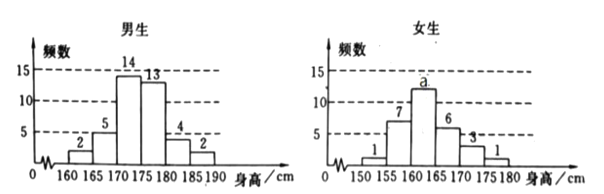
(1)估计该校男生的人数;并求出![]() 值
值
(2)估计该校学生身高在![]() 之间的概率;
之间的概率;
(3)从样本中身高在![]() 之间的女生中任选2人,求至少有1人身高在
之间的女生中任选2人,求至少有1人身高在![]() 之间的概率。
之间的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com