
对于各项均为整数的数列![]() ,如果
,如果![]() (
(![]() =1,2,3,…)为完全平方数(即能表示为一个整数的平方的数,例如4是完全平方数、3不是完全平方数),则称数列
=1,2,3,…)为完全平方数(即能表示为一个整数的平方的数,例如4是完全平方数、3不是完全平方数),则称数列![]() 具有“
具有“![]() 性质”.不论数列
性质”.不论数列![]() 是否具有“
是否具有“![]() 性质”,如果存在与
性质”,如果存在与![]() 不是同一数列的
不是同一数列的![]() ,且
,且![]() 同时满足下面两个条件:①
同时满足下面两个条件:①![]() 是
是![]() 的一个排列;②数列
的一个排列;②数列![]() 具有“
具有“![]() 性质”,则称数列
性质”,则称数列![]() 具有“变换
具有“变换![]() 性质”.下面三个数列:①数列
性质”.下面三个数列:①数列![]() 的前
的前![]() 项和
项和![]() ;②数列1,2,3,4,5;③1,2,3,…,11.具有“
;②数列1,2,3,4,5;③1,2,3,…,11.具有“![]() 性质”的为 ;具有“变换
性质”的为 ;具有“变换![]() 性质”的为 .
性质”的为 .
科目:高中数学 来源: 题型:
| n | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n | 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海市浦东新区高三第三次模拟理科数学试卷(解析版) 题型:填空题
定义:对于各项均为整数的数列 ,如果
,如果 (
( =1,2,3, )为完全平方数,则称数列
=1,2,3, )为完全平方数,则称数列 具有“
具有“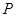 性质”;不论数列
性质”;不论数列 是否具有“
是否具有“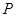 性质”,如果存在数列
性质”,如果存在数列 与
与 不是同一数列,且
不是同一数列,且 满足下面两个条件:
满足下面两个条件:
(1) 是
是 的一个排列;
的一个排列;
(2)数列 具有“
具有“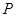 性质”,则称数列
性质”,则称数列 具有“变换
具有“变换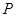 性质”.
性质”.
给出下面三个数列:
①数列 的前
的前 项和
项和 ;
;
②数列 :1,2,3,4,5;
:1,2,3,4,5;
③数列 :1,2,3,4,5,6,7,8,9,10,11.
:1,2,3,4,5,6,7,8,9,10,11.
具有“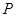 性质”的为 ;具有“变换
性质”的为 ;具有“变换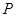 性质”的为 .
性质”的为 .
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省高三10月月考理科数学试卷(解析版) 题型:填空题
对于各项均为整数的数列 ,如果
,如果 (
( =1,2,3,…)为完全平方数,则称数
=1,2,3,…)为完全平方数,则称数
列 具有“
具有“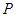 性质”.不论数列
性质”.不论数列 是否具有“
是否具有“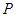 性质”,如果存在与
性质”,如果存在与 不是同一数列的
不是同一数列的 ,且
,且 同时满足下面两个条件:①
同时满足下面两个条件:① 是
是 的一个排列;②数列
的一个排列;②数列 具有“
具有“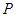 性质”,则称数列
性质”,则称数列 具有“变换
具有“变换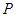 性质”.下面三个数列:①数列
性质”.下面三个数列:①数列 的前
的前 项和
项和 ;②数列1,2,3,4,5;③1,2,3,…,11.具有“
;②数列1,2,3,4,5;③1,2,3,…,11.具有“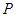 性质”的为
;具有“变换
性质”的为
;具有“变换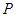 性质”的为
.
性质”的为
.
查看答案和解析>>
科目:高中数学 来源:北京市西城区2010年高三一模数学(理)试题 题型:解答题
(本小题满分13分)
对于各项均为整数的数列 ,如果
,如果 (
( =1,2,3,…)为完全平方数,则称数
=1,2,3,…)为完全平方数,则称数
列 具有“
具有“ 性质”。
性质”。
不论数列 是否具有“
是否具有“ 性质”,如果存在与
性质”,如果存在与 不是同一数列的
不是同一数列的 ,且
,且 同
同
时满足下面两个条件:① 是
是 的一个排列;②数列
的一个排列;②数列 具有“
具有“ 性质”,则称数列
性质”,则称数列 具有“变换
具有“变换 性质”。
性质”。
(I)设数列 的前
的前 项和
项和 ,证明数列
,证明数列 具有“
具有“ 性质”;
性质”;
(II)试判断数列1,2,3,4,5和数列1,2,3,…,11是否具有“变换 性质”,具有此性质的数列请写出相应的数列
性质”,具有此性质的数列请写出相应的数列 ,不具此性质的说明理由;
,不具此性质的说明理由;
(III)对于有限项数列 :1,2,3,…,
:1,2,3,…, ,某人已经验证当
,某人已经验证当 时,
时,
数列 具有“变换
具有“变换 性质”,试证明:当”
性质”,试证明:当” 时,数列
时,数列 也具有“变换
也具有“变换 性质”。
性质”。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com