
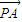 |-|
|-|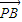 |=4,|
|=4,| -
-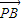 |=10,
|=10,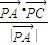 =
=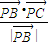 ,且
,且 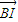 =
=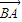 +λ(
+λ(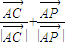 ),(λ>0),
),(λ>0),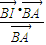 的值为( )
的值为( )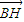 |=
|= (|
(|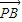 |+|
|+|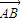 |-|
|-|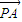 |)=3,结合向量数量积的运算公式和直角三角形中三角函数的定义,可得
|)=3,结合向量数量积的运算公式和直角三角形中三角函数的定义,可得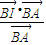 =
=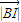 cos∠IBH=
cos∠IBH=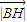 =3.
=3. ,
,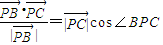

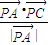 =
=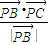 ,得cos∠APC=cos∠BPC,
,得cos∠APC=cos∠BPC,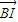 =
=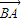 +λ(
+λ(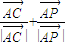 ),(λ>0),
),(λ>0),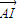 =λ(
=λ(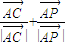 ),(λ>0),得I在∠CAP的平分线上
),(λ>0),得I在∠CAP的平分线上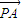 |-|
|-|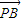 |=4,|
|=4,| -
-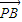 |=|
|=|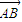 |=10,
|=10,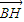 |=|
|=|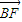 |=
|= (|
(|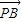 |+|
|+|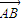 |-|
|-|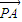 |)=
|)= [|
[|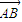 |-(|
|-(|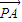 |-|
|-|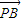 |)]=3
|)]=3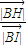 ,
, =
=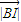 cos∠IBH=
cos∠IBH= =3
=3

科目:高中数学 来源: 题型:
 选考题
选考题| 1 | ||
|
|
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
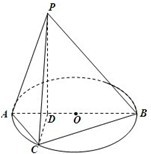 (2013•佛山一模)如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且AD=
(2013•佛山一模)如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且AD=| 1 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
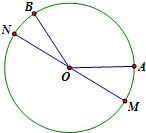 已知A,B是单位圆上的两点,O为圆心,且∠AOB=120°,MN是圆O的一条直径,点C在圆内,且满足
已知A,B是单位圆上的两点,O为圆心,且∠AOB=120°,MN是圆O的一条直径,点C在圆内,且满足| OC |
| OA |
| OB |
| CM |
| CN |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com