
| 7 |
| 9 |
| 19a |
| 72 |
| 19a |
| 72 |
| 1 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 19 |
| 72 |
| 7 |
| 9 |
| 5 |
| 4 |
| 5 |
| 4 |
| 19 |
| 72 |
| 7 |
| 9 |
| 5 |
| 4 |
| lg5 |
| lg5-2lg2 |
| 1-lg2 |
| 1-3lg2 |
| 5 |
| 4 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
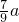 ,如果
,如果 ,那么该地区今后会发生水土流失吗?若会,需要经过几年?(参考数据:lg2=0.3)
,那么该地区今后会发生水土流失吗?若会,需要经过几年?(参考数据:lg2=0.3)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第25课时):第三章 数列-数列的实际应用(解析版) 题型:解答题
 ,如果
,如果 ,那么该地区今后会发生水土流失吗?若会,需要经过几年?(参考数据:lg2=0.3)
,那么该地区今后会发生水土流失吗?若会,需要经过几年?(参考数据:lg2=0.3)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com