已知:一动圆过B(1,0)且与圆A:x2+y2+2x+4λ-3=0(0<λ<1)相切.
(1)证明动圆圆心P的轨迹是双曲线,并求其方程;
(2)过点B作直线l交双曲线右支于M、N两点,是否存在λ的值,使得△AMN成为以∠ANM为直角的等腰三角形,若存在则求出λ的值,若不存在则说明理由.
【答案】
分析:(1)当动圆与圆A内切时,|PA|-|PB|=2
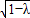
;当动圆与圆A外切时,|PB|-|PA|=2
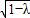
,利用双曲线的定义可得结论;
(2)若过点B作直线l垂直于x轴,则△AMN不可能成为以∠ANM为直角的等腰三角形;若过点B作直线l不垂直于x轴,则设l的方程与
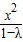
-
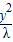
=1联立,确定N的坐标,可得直线l的斜率,利用直线l与双曲线右支有两个交点,可得λ的取值范围,利用|AN|=|MN|,即可求得结论.
解答:(1)证明:圆A:x
2+y
2+2x+4λ-3=0可化为(x+1)
2+y
2=4(1-λ),圆心为(-1,0),半径为r=2
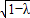
当动圆与圆A内切时,|PA|-|PB|=2
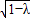
;当动圆与圆A外切时,|PB|-|PA|=2
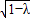
;
∴||PB|-|PA||=2
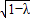
,
∵0<λ<1,∴2
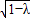
<2
∴||PB|-|PA||<|AB|
∴动圆圆心P的轨迹是双曲线,其方程为
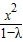
-
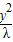
=1;
(2)解:若过点B作直线l垂直于x轴,则△AMN不可能成为以∠ANM为直角的等腰三角形;
若过点B作直线l不垂直于x轴,则设l:y=k(x-1),l与双曲线右支交于M(x
1,y
1),N(x
2,y
2)两点
∵∠ANM为直角,∴N在以AB为直径的圆x
2+y
2=1上
与
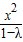
-
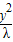
=1联立,解得x=±
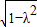
,y=±λ
∵N在右支上,∴N(

,±λ)
不妨设N在x轴下方,∴N(
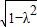
,-λ)
此时,直线l的斜率为k=
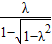
①
|AN|=
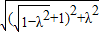
=
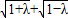
y=k(x-1)代入
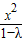
-
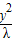
=1,可得[λ-(1-λ)k
2]x
2+2(1-λ)k
2x-(1-λ)(λ+k
2)=0②
∵直线l与双曲线右支有两个交点,∴
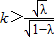
,∴λ-(1-λ)k
2<0③
于是x
1+x
2=
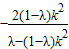
,x
1x
2=
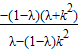
将①代入③,可得λ的取值范围为(0,

)
∴|MN|=
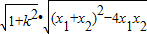
=
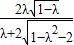
-2
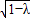
∵|AN|=|MN|,∴
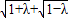
=
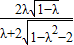
-2
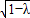
∴17λ
2-24λ+8=0,∴λ=
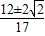
∵λ∈(0,

)
∴存在λ=
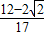
,使得△AMN成为以∠ANM为直角的等腰三角形.
点评:本题考查轨迹方程,考查双曲线的定义,考查直线与曲线的位置关系,考查存在性问题,考查学生分析解决问题的能力,属于中档题.

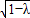 ;当动圆与圆A外切时,|PB|-|PA|=2
;当动圆与圆A外切时,|PB|-|PA|=2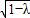 ,利用双曲线的定义可得结论;
,利用双曲线的定义可得结论;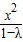 -
-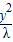 =1联立,确定N的坐标,可得直线l的斜率,利用直线l与双曲线右支有两个交点,可得λ的取值范围,利用|AN|=|MN|,即可求得结论.
=1联立,确定N的坐标,可得直线l的斜率,利用直线l与双曲线右支有两个交点,可得λ的取值范围,利用|AN|=|MN|,即可求得结论.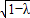
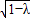 ;当动圆与圆A外切时,|PB|-|PA|=2
;当动圆与圆A外切时,|PB|-|PA|=2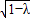 ;
;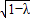 ,
,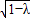 <2
<2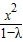 -
-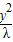 =1;
=1;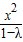 -
-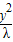 =1联立,解得x=±
=1联立,解得x=±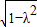 ,y=±λ
,y=±λ ,±λ)
,±λ)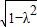 ,-λ)
,-λ)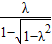 ①
①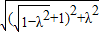 =
=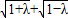
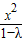 -
-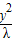 =1,可得[λ-(1-λ)k2]x2+2(1-λ)k2x-(1-λ)(λ+k2)=0②
=1,可得[λ-(1-λ)k2]x2+2(1-λ)k2x-(1-λ)(λ+k2)=0②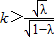 ,∴λ-(1-λ)k2<0③
,∴λ-(1-λ)k2<0③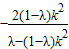 ,x1x2=
,x1x2=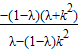
 )
)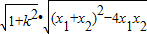 =
=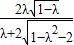 -2
-2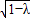
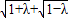 =
=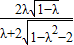 -2
-2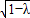
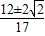
 )
)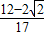 ,使得△AMN成为以∠ANM为直角的等腰三角形.
,使得△AMN成为以∠ANM为直角的等腰三角形.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案