
【题目】已知函数f(x)=x2+2mx+3m+4,
(1)若f(x)在(﹣∞,1]上单调递减,求m的取值范围;
(2)求f(x)在[0,2]上的最大值g(m).
【答案】
(1)解:∵函数f(x)=x2+2mx+3m+4,
∴f(x)的对称轴是x=﹣m,
又∵f(x)在(﹣∞,1]上单调递减,
∴﹣m≥1,解得m≤﹣1,
∴m的取值范围是(﹣∞,﹣1]
(2)解:f(x)的对称轴为x=﹣m
当﹣m≥1,即m≤﹣1时,
f(x)在[0,2]上的最大值g(m)=f(0)=3m+4,
当﹣m<1,即m>﹣1时,
f(x)在[0,2]上的最大值g(m)=f(2)=7m+8,
∴ ![]()
【解析】(1)由f(x)的对称轴是x=﹣m,f(x)在(﹣∞,1]上单调递减,得﹣m≥1,由此能求出m的取值范围.(2)由f(x)的对称轴为x=﹣m,根据m≤﹣1和m>﹣1两种情况分类讨论能求出f(x)在[0,2]上的最大值g(m).
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x+2 ![]() sinxcosx+sin(x+
sinxcosx+sin(x+ ![]() )sin(x﹣
)sin(x﹣ ![]() ),x∈R.
),x∈R.
(1)求f(x)的最小正周期和单调增区间;
(2)若x=x0(0≤x0≤ ![]() )为f(x)的一个零点,求cos2x0的值.
)为f(x)的一个零点,求cos2x0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,a2=2,an+2=(1+cos2 ![]() )an+sin2
)an+sin2 ![]() ,则该数列的前12项和为( )
,则该数列的前12项和为( )
A.211
B.212
C.126
D.147
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax﹣(k﹣1)a﹣x(a>0且a≠1)是定义域为R的奇函数.
(1)求k值;
(2)若f(1)<0,试判断y=f(x)的单调性并求使不等式f(x2+tx)+f(4﹣x)<0恒成立的t的取值范围;
(3)若f(1)= ![]() ,g(x)=a2x+a﹣2x﹣2f(x),求k∈N+在[1,+∞)上的最小值.
,g(x)=a2x+a﹣2x﹣2f(x),求k∈N+在[1,+∞)上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个人以6米/秒的匀速度去追赶停在交通灯前的汽车,当他离汽车25米时交通灯由红变绿,汽车开始作变速直线行驶(汽车与人的前进方向相同),汽车在时刻t的速度为v(t)=t米/秒,那么,此人( )
A.可在7秒内追上汽车
B.可在9秒内追上汽车
C.不能追上汽车,但其间最近距离为14米
D.不能追上汽车,但其间最近距离为7米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下:
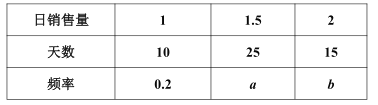
若以上表中频率作为概率,且每天的销售量相互独立.
(1)求5天中该种商品恰好有两天的日销售量为1.5吨的概率;
(2)已知每吨该商品的销售利润为2千元, ![]() 表示该种商品某两天销售利润的和(单位:千元),求
表示该种商品某两天销售利润的和(单位:千元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com