
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 与
与![]() 恰有一个公共点.
恰有一个公共点.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)已知曲线![]() 上两点
上两点![]() ,
,![]() 满足
满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,底面ABCD是梯形,AB∥DC,AD⊥DC,AB=AD=2,DC=3,平面PDC⊥平面ABCD,E在棱PC上且PE=2EC。
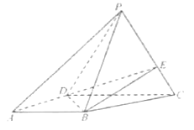
()证明:BE∥平面PAD;
(1)若ΔPDC是正三角形,求三棱锥P-DBE的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蔬菜批发市场销售某种蔬菜,在一个销售周期内,每售出1吨该蔬菜获利500元,未售出的蔬菜低价处理,每吨亏损100元.统计该蔬菜以往100个销售周期的市场需求量,绘制下图所示频率分布直方图.
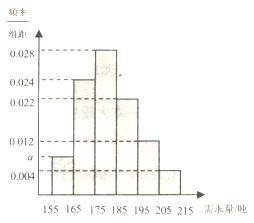
(Ⅰ)求![]() 的值,并求100个销售周期的平均市场需求量(以各组的区间中点值代表该组的数值);
的值,并求100个销售周期的平均市场需求量(以各组的区间中点值代表该组的数值);
(Ⅱ)若经销商在下个销售周期购进了190吨该蔬菜,设![]() 为该销售周期的利润(单位:元),
为该销售周期的利润(单位:元),![]() 为该销售周期的市场需求量(单位:吨).求
为该销售周期的市场需求量(单位:吨).求![]() 与
与![]() 的函数解析式,并估计销售的利润不少于86000元的概率.
的函数解析式,并估计销售的利润不少于86000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是函数
是函数![]() 的导函数,且
的导函数,且![]() ,
,![]() ,则下列说法正确的是___________.
,则下列说法正确的是___________.
①![]() ;
;
②曲线![]() 在
在![]() 处的切线斜率最小;
处的切线斜率最小;
③函数![]() 在
在![]() 存在极大值和极小值;
存在极大值和极小值;
④![]() 在区间
在区间![]() 上至少有一个零点.
上至少有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2020年举行促销活动,经调查测算,某产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元,满足
万元,满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2020年生产该产品的固定投入为8万元,每生产1万件,该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2020年生产该产品的固定投入为8万元,每生产1万件,该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2020年该产品的利润![]() (万元)表示为年促销费用
(万元)表示为年促销费用![]() (万元)的函数;
(万元)的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数据![]() 是宜昌市
是宜昌市![]() 个普通职工的年收入,设这
个普通职工的年收入,设这![]() 个数据的中位数为
个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,则这
,则这![]() 个数据中,下列说法正确的是( )
个数据中,下列说法正确的是( )
A. 年收入平均数可能不变,中位数可能不变,方差可能不变
B. 年收入平均数大大增大,中位数可能不变,方差变大
C. 年收入平均数大大增大,中位数可能不变,方差也不变
D. 年收入平均数大大增大,中位数一定变大,方差可能不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com