解:(1)将不等式去绝对值,化简为:
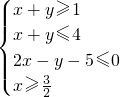
或

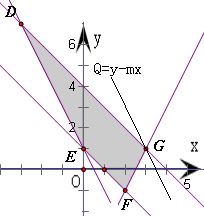
平面区域为如图所示的四边形DEFG及其内部,其中D(-3,7),E(0,1),F(2,-1),G(3,1);
由图可知,当动点(x,y)与点D(-3,7)重合时,
x
2+y
2达到最大值,最大值为OD
2=9+49=58;
当动点(x,y)与原点在直线EF上的射影重合时,
x
2+y
2达到最小值,最小值为

∴x
2+y
2的取值范围是[

,58]
(2)作直线l:Q=y-mx,则它的斜率k=m(k>-1)
运动直线l,并观察图形可得:
①当-1<k≤2即-1<m≤2时
平移l到经过D点时,Q=y-mx值最大,Q
max=7+3m;
平移l到经过F点时,Q=y-mx值最小Q
min=-1-2m
②当k>2,即m>2时,
平移l到经过D点时,Q=y-mx值最大,Q
max=7+3m
平移l到经过G点时,Q=y-mx值最小Q
min=1-3m.
分析:(1)将不等式去绝对值化简,即可作出如图的四边形DEFG及其内部,即为所求平面区域.再根据原点到点(x,y)的距离,算出x
2+y
2的最大最小值,即可得到x
2+y
2的取值范围;
(2)作直线l:Q=y-mx并进行平移,观察图形可得:Q的最大值为7+3m;当-1<k≤2时Q的最小值为-1-2m,当k>2时Q的最小值为1-3m.
点评:本题给出二元一次不等式组,求作平面区域并求目标函数的最大最小值,着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识,属于中档题.

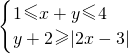 .
.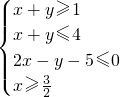 或
或


 ,58]
,58]

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案