
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,若过点F且斜率为1的直线与抛物线相交于M,N两点,且|MN|=8.
(1)求抛物线C的方程;
(2)设直线l为抛物线C的切线,且l∥MN,P为l上一点,求 ![]() 的最小值.
的最小值.
【答案】
(1)解:由题可知 ![]() ,则该直线方程为:
,则该直线方程为: ![]() ,
,
代入y2=2px(p>0)得: ![]() ,
,
设M(x1,y1),N(x2,y2),则有x1+x2=3p
∵|MN|=8,∴x1+x2+p=8,即3p+p=8,解得p=2
∴抛物线的方程为:y2=4x.

(2)解:设l方程为y=x+b,代入y2=4x,得x2+(2b﹣4)x+b2=0,
∵l为抛物线C的切线,∴△=0,
解得b=1,∴l:y=x+1
由(1)可知:x1+x2=6,x1x2=1
设P(m,m+1),则 ![]()
∴ ![]()
= ![]()
∵x1+x2=6,x1x2=1, ![]() ,y1y2=﹣4,
,y1y2=﹣4, ![]() ,
,
∴ ![]() ,
,
∴ ![]()
=2[m2﹣4m﹣3]=2[(m﹣2)2﹣7]≥﹣14
当且仅当m=2时,即点P的坐标为(2,3)时, ![]() 的最小值为﹣14.
的最小值为﹣14.
【解析】(1)过点F且斜率为1的直线代入抛物线,利用|MN|=8,可得x1+x2+p=8,即可求抛物线C的方程;(2)设l方程为y=x+b,代入y2=4x,利用直线l为抛物线C的切线,求出b,再利用向量的数量积公式求 ![]() ,利用配方法可求最小值.
,利用配方法可求最小值.


科目:高中数学 来源: 题型:
【题目】【2016-2017学年度苏锡常镇四市高三教学情况调研(二)】某科研小组研究发现:一棵水蜜桃树的产量![]() (单位:百千克)与肥料费用
(单位:百千克)与肥料费用![]() (单位:百元)满足如下关系:
(单位:百元)满足如下关系:![]() ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)![]() 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求利润函数![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某大学一年级女生中,选取身高分别是150cm、155cm、160cm、165cm、170cm的学生各一名,其身高和体重数据如表所示:
身高/cm(x) | 150 | 155 | 160 | 165 | 170 |
体重/kg(y) | 43 | 46 | 49 | 51 | 56 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,计算身高为168cm时,体重的估计值 ![]() 为多少?
为多少?
参考公式:线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =
=  =
= 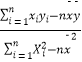 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 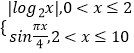 .
.
(1)设函数g(x)=f(x)﹣1,求函数g(x)的零点;
(2)若函数f(x1)=f(x2)=f(x3)=f(x4),且0<x1<x2<x3<x4≤10,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x2+y2﹣4x﹣2y﹣k=0表示图形为圆.
(1)若已知曲线关于直线x+y﹣4=0的对称圆与直线6x+8y﹣59=0相切,求实数k的值;
(2)若k=15,求过该曲线与直线x﹣2y+5=0的交点,且面积最小的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四面体ABCD中,E、F分别是AC、BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成的角为( )
A.90°
B.45°
C.60°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正三棱锥P﹣ABC底面边长为6,底边BC在平面α内,绕BC旋转该三棱锥,若某个时刻它在平面α上的正投影是等腰直角三角形,则此三棱锥高的取值范围是( ) 
A.(0, ![]() ]
]
B.(0, ![]() ]∪[
]∪[ ![]() ,3]
,3]
C.(0, ![]() ]
]
D.(0, ![]() ]∪[3,
]∪[3, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—5:不等式选讲]
已知函数f(x)=–x2+ax+4,g(x)=│x+1│+│x–1│.
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[–1,1],求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com