练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知∠AOB＝60°，过点O引∠AOB所在平面的斜线OC与OA、OB均成60°，求二面角A－OC－B的平面角的正弦值．

    答案：
    解析：

    　　解：如下图，在OC上任取一点D，在平面COB内作DE⊥OC交OB于E，在平面AOC内作DF⊥OC交OA于F，

    　　

    　　思路分析：本题考查利用二面角的平面角的定义求二面角大小的方法，由于OA、OB、OC均为射线，二面角的平面角的顶点无论取在何处，均能与已知条件取得联系．

    　　温馨提示：根据二面角的平面角的定义直接作出二面角的平面角是最基本和最常用的方法之一，即过棱上任意一点分别在两个半平面内作棱的垂线，所得的角就是二面角的平面角．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：广东省梅县东山中学2011－2012学年高二上学期期中考试数学文科试题 题型：022

    已知∠AOB＝90°，过O点引∠AOB所在平面的斜线OC，OC与OA、OB分别成45°、60°，则以OC为棱的二面角A－OC－B的余弦值等于________

    查看答案和解析>>

    科目：高中数学 来源：2008年普通高等学校招生全国统一考试(四川延考卷)、数学试题及答案(理科) 题型：022

    已知∠AOB＝90°，C为空间中一点，且∠AOC＝∠BOC＝60°，则直线OC与平面AOB所成角的正弦值为________．

    查看答案和解析>>

    科目：高中数学 来源：2008年普通高等学校招生全国统一考试(四川延考卷)、数学试题用答案(文科) 题型：022

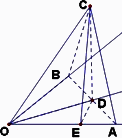
    已知∠AOB＝90°，C为空间中一点，且∠AOC＝∠BOC＝60°，则直线OC与平面AOB所成角的正弦值为________．

    查看答案和解析>>

    科目：高中数学 来源：新课标高三数学空间向量及其运算、角的概念及其求法和空间距离专项训练（河北） 题型：填空题

    已知∠AOB＝90°，C为空间中一点，且∠AOC＝∠BOC＝60°，则直线OC与平面AOB所成角的正弦值为_________                

     

    查看答案和解析>>

    同步练习册答案