Question

如果奇函数f（x）是定义域（-1，1）上的减函数，且f（1-m）+f（1-m²）＜0，求实数m的取值范围．

Answer 1

解：因为函数f（x）的定义域是（-1，1）
所以有-1＜1-m＜1 ①
-1＜1-m²＜1 ②
又f（x）是奇函数，所以f（1-m）+f（1-m²）＞0可变为f（1-m）＞f（m²-1）
又f（x）在（-1，1）内是减函数，所以1-m＜m²-1 ③
由①、②、③得 ．
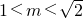
分析：根据定义域先建立两个不等关系式，再结合函数的单调性和奇偶性建立关系式，解之即可．
点评：本题主要考查了函数单调性与奇偶性的应用，以及不等式的求解，属于中档题．