
(本小题14分)
某创业投资公司拟投资开发某种新能源产品,估计能获得10万元~1000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)若建立函数模型制定奖励方案,试用数学语言表述公司对奖励函数模型的基本要求;
(2)现有两个奖励函数模型:(1)y=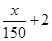 ;(2)y=4lgx-3.试分析这两个函数模型是否符合公司要求?
;(2)y=4lgx-3.试分析这两个函数模型是否符合公司要求?
(1)当x∈[10,1000]时,①f(x)是增函数;②f(x)≤9恒成立;③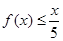 恒成立
恒成立
(2)所以g(x)在[10,1000]上是减函数,从而g(x)≤g(10)=-1<0.
所以4lgx-3-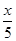 <0,即4lgx-3<
<0,即4lgx-3<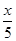 ,所以
,所以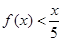 恒成立
恒成立
【解析】解:(1)设奖励函数模型为y=f(x),则公司对函数模型的基本要求是:
当x∈[10,1000]时,①f(x)是增函数;②f(x)≤9恒成立;③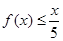 恒成立…5分
恒成立…5分
(2)①对于函数模型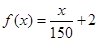 :
:
当x∈[10,1000]时,f(x)是增函数, …………………… 6分
则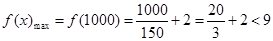 .所以f(x)≤9恒成立.… 8分
因为函数
.所以f(x)≤9恒成立.… 8分
因为函数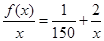 在[10,1000]上是减函数,所以
在[10,1000]上是减函数,所以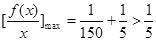 .
.
从而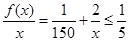 ,即
,即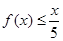 不恒成立.
不恒成立.
故该函数模型不符合公司要求. ………………………… 10分
②对于函数模型f(x)=4lgx-3:
当x∈[10,1000]时,f(x)是增函数, …………… 11分
则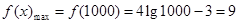 .所以f(x)≤9恒成立.……… 13分
.所以f(x)≤9恒成立.……… 13分
设g(x)=4lgx-3-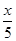 ,则
,则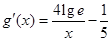 .
.
当x≥10时,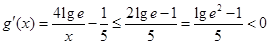 ,
,
所以g(x)在[10,1000]上是减函数,从而g(x)≤g(10)=-1<0.
所以4lgx-3-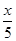 <0,即4lgx-3<
<0,即4lgx-3<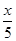 ,所以
,所以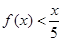 恒成立.
恒成立.
故该函数模型符合公司要求.………………………… 15分


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源:2014届广东省高二第一次阶段考试理科数学试卷(解析版) 题型:解答题
(本小题14分)某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大已知对这两种产品有直接限制的因素是资金和劳动力,通过调查,得到关于这两种产品的有关数据如下表:
|
资 金 |
单位产品所需资金(百元) |
月资金供应量(百元) |
|
|
空调机 |
洗衣机 |
||
|
成 本 |
30 |
20 |
300 |
|
劳动力(工资) |
5 |
10 |
110 |
|
单位利润 |
6 |
8 |
|
试问:怎样确定两种货物的月供应量,才能使总利润达到最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三上学期第一次调研考试数学试卷(实验班) 题型:解答题
(本小题14分)某企业生产A、B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如左图, B产品的利润与投资的算术平方根成正比,其关系如右图 (注:利润与投资单位:万元).
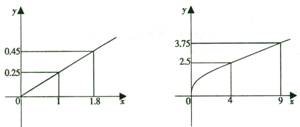
(1)分别将A、B两种产品的利润表示为投资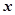 (万元)的函数关系式;
(万元)的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省肇庆市高三复习必修五综合练习 题型:解答题
(本小题14分)某工厂要制造A种电子装置41台,B种电子装置66台,需用薄钢板给每台装置配一个外壳,已知薄钢板的面积有两种规格:甲种薄钢板每张面积2㎡,可做A、B的外壳分别为2个和7个,乙种薄钢板每张面积5㎡,可做A、B的外壳分别为7个和9个,求两种薄钢板各用多少张,才能使总的用料面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题14分)
某化工厂生产某种产品,每件产品的生产成本是3元,根据市场调查,预计每件产品的出厂价为x元(7≤x≤10)时,一年的产量为(11-x)2万件;若该企业所生产的产品全部销售,则称该企业正常生产;但为了保护环境,用于污染治理的费用与产量成正比,比例系数为常数k (1≤k≤3)。
(1)求该企业正常生产一年的利润F(x)与出厂价x的函数关系式;
(2)当每件产品的出厂价定为多少元时,企业一年的利润最大,并求最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com