
已知两点F1(-1,0)及F2(1,0),点P在以F1、F2为焦点的椭圆C上,且|PF1|、|F1F2|、|PF2|构成等差数列.
(1)求椭圆C的方程;
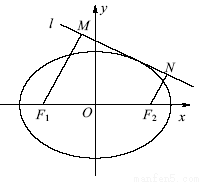
(2)如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且F1M⊥l,F2N⊥l.求四边形F1MNF2面积S的最大值.
(1)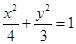 ;(2)
;(2)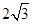 。
。
【解析】
试题分析:(1)依题意,设椭圆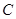 的方程为
的方程为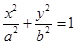 .
.
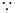
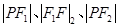 构成等差数列,
构成等差数列,
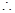
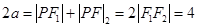 ,
, 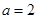 .
.
又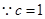 ,
,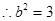 .
.
 椭圆
椭圆 的方程为
的方程为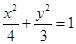 . 4分
. 4分
(2) 将直线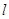 的方程
的方程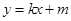 代入椭圆
代入椭圆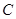 的方程
的方程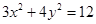 中,得
中,得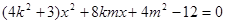 . 5分
. 5分
由直线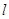 与椭圆
与椭圆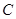 仅有一个公共点知,
仅有一个公共点知,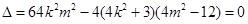 ,
,
化简得: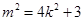 . 7分
. 7分
设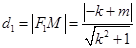 ,
,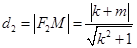 , 9分
, 9分
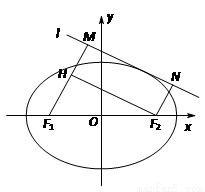
(法一)当 时,设直线
时,设直线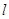 的倾斜角为
的倾斜角为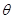 ,
,
则 ,
,
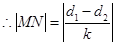 ,
,
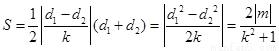
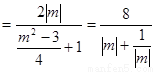 ,11分
,11分
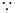
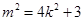 ,
,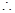 当
当 时,
时,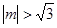 ,
,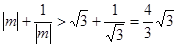 ,
,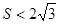 .
.
当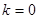 时,四边形
时,四边形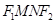 是矩形,
是矩形,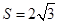 . 13分
. 13分
所以四边形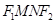 面积
面积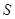 的最大值为
的最大值为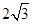 . 14分
. 14分
(法二)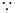
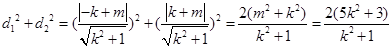 ,
,
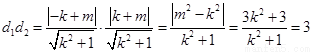 .
.
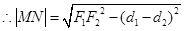
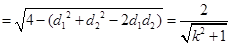 .
.
四边形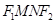 的面积
的面积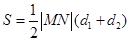
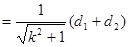 , 11分
, 11分
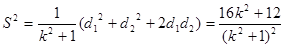
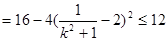 . 13分
. 13分
当且仅当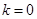 时,
时, ,故
,故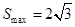 .
.
所以四边形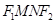 的面积
的面积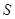 的最大值为
的最大值为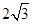 . 14分
. 14分
考点:椭圆的标准方程;椭圆的简单性质;椭圆的定义;直线与椭圆的综合应用;基本不等式。
点评:(1)本题主要考查椭圆的方程与性质、直线方程、直线与椭圆的位置关系等基础知
识,考查学生运算能力、推理论证以及分析问题、解决问题的能力,考查分类讨论、数形结合、化归与转化思想.(2)做此题的关键是表示出四边形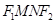 的面积。本题在计算过程中较为复杂繁琐,我们在计算的过程中一定要耐住性子,认真、细致,避免出现计算错误。
的面积。本题在计算过程中较为复杂繁琐,我们在计算的过程中一定要耐住性子,认真、细致,避免出现计算错误。


科目:高中数学 来源: 题型:
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•深圳一模)已知两点F1(-1,0)及F2(1,0),点P在以F1、F2为焦点的椭圆C上,且|PF1|、|F1F2|、|PF2|构成等差数列.
(2013•深圳一模)已知两点F1(-1,0)及F2(1,0),点P在以F1、F2为焦点的椭圆C上,且|PF1|、|F1F2|、|PF2|构成等差数列.查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省成都市六校协作体高二(上)期中数学试卷(理科)(解析版) 题型:选择题
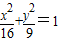
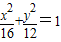
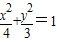
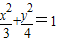
查看答案和解析>>
科目:高中数学 来源:2010-2011学年陕西省西安一中高二(上)期末数学试卷(理科)(解析版) 题型:选择题
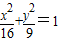
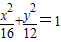
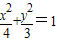
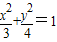
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com