Question

22．已知点是抛物线上的两个动点，是坐标原点，向量满足，设圆的方程为．

（1）证明线段是圆的直径；

（2）当圆的圆心到直线的距离的最小值为时，求的值．

Answer 1

本小题主要考查平面向量的基本运算，圆与抛物线的方程，点到直线的距离等基础知识，以及综合运用解析几何知识解决问题的能力.

（Ⅰ）证法一：∵.

∴，即

²+2·+²=²-2·+².整理得

·=0，

∴x₁x₃+y₁y₃=0.                                   ①

设点M（x，y）是以线段AB为直径的圆上的任意一点，则

·=0，

即

（x-x₁）（x-x₂）+（y-y₁）（y-y₂）=0.

展开上式并将①代入得

x³+y²=（x₁+x₂）x-（y₁+y₂）y=0.

故线段AB是圆C的直径.

证法二：∵|+|=|-|，

∴（+）²=（-）²，即

  ²+2·+²=²-2·+².整理得

·=0，

∴x₁x₂+y₁y₂=0.                                   ①

若点（x，y）在以线段AB为直径的圆上，则

       =-1，（x≠x₁，x≠x₂）

去分母得

   （x-x₁）（x-x₂）+（y-y₁）（y-y₂）=0.

点（x₁，y₁），（x₁，y₂），（x₂，y₁），（x₂，y₂）满足上方程，展开并将①代入得

x²+y²-（x₁+x₂）x-（y₁+y₂）y=0.

所以线段AB是圆C的直径.

证法三：∵|+|=|-|，

∴（+）²=（-）²，即

²+2·+²=²-2·+²,整理得

·=0，

∴x₁x₂+y₁y₂=0.                                   ①

以AB为直径的圆的方程是

（x-）²+（y-）²=［（x₁-x₂）²+（y₁-y₂）²］，

展开，并将①代入得

x²+y²-（x₁+x₂）x-（y₁₊y₂）y=0，

所以线段AB是圆C的直径.

（Ⅱ）解法一：设圆C的圆心为C（x，y），则

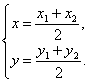
∵y₁²=2px₁，y₂²=2px₂（p＞0），

∴x₁x₂=，

又∵x₁x₂+y₁y₂=0.

∴x₁x₂=-y₁y₂，

∴-y₁y₂=，

∵x₁x₂≠0，

∴y₁y₂≠0，

∴y₁y₂=-4p².

∴x=

   =

   =.

所以圆心的轨迹方程为：

y²=px-2p².

设圆心C到直线x-2y=0的距离为d，则

d=

 =

 =.

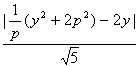
当y=p时，d有最小值，由题设得

，

∴p=2.

解法二：设圆C的圆心为C（x，y），则

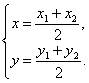
∵y₁²=2px₁，y₂²=2px₂（p＞0），

∴x₁x₂=.

又∵x₁x₂+y₁y₂=0，

∴x₁x₂=-y₁y₂，

∵x₁x₂≠0，

∴y₁y₂=-4p²，

∵x=

   =）

   =

   =.

所以圆心的轨迹方程为

y²=px-2p².

设直线x-2y+m=0与x-2y=0的距离为，则

m=±2.

因为x-2y+2=0与y²=px-2p²无公共点，

所以当x-2y-2=0与y²=px-2p²仅有一个公共点时，该点到x-2y=0的距离最小，最小值为.

将②代入③得

y²-2py+2p²-2p=0.有

△=4p²-4（2p²-2p）=0.

∵p＞0，

∴p=2.

解法三：设圆C的圆心为C（x，y），则

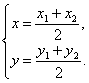
若圆心C到直线x-2y=0的距离为d，那么

d=.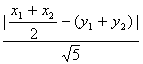

∵y₁²=2px₁，y₂²=2px₂（p＞0），

∴x₁x₂=.

又∵x₁x₂+y₁y₂=0，

∴x₁x₂=-y₁y₂，

∵x₁x₂≠0，

∴y₁y₂=-4p².

∴d=

   =

   =.

当y₁+y₂=2p时，d有最小值，由题意得

，

∴p=2.