
(06年辽宁卷)(14分)
已知点![]() 是抛物线
是抛物线![]() 上的两个动点,
上的两个动点,![]() 是坐标原点,向量
是坐标原点,向量![]() 满足
满足![]() ,设圆
,设圆![]() 的方程为
的方程为![]() .
.
(1)证明线段![]() 是圆
是圆![]() 的直径;
的直径;
(2)当圆![]() 的圆心到直线
的圆心到直线![]() 的距离的最小值为
的距离的最小值为![]() 时,求
时,求![]() 的值.
的值.
解析:(I)证法一:![]()
![]()
即![]()
整理得![]()
![]() ......................12分
......................12分
设点M(x,y)是以线段AB为直径的圆上的任意一点,则![]()
即![]()
展开上式并将①代入得![]()
故线段![]() 是圆
是圆![]() 的直径。
的直径。
证法二:![]()
![]()
即![]() ,
,
整理得![]()
![]() ①……3分
①……3分
若点![]() 在以线段
在以线段![]() 为直径的圆上,则
为直径的圆上,则![]()
去分母得![]()
点![]() 满足上方程,展开并将①代入得
满足上方程,展开并将①代入得
![]()
所以线段![]() 是圆
是圆![]() 的直径.
的直径.
证法三:
![]()
![]()
![]()
即![]() ,
,
整理得![]()
![]()
以![]() 为直径的圆的方程是
为直径的圆的方程是![]()
展开,并将①代入得![]()
所以线段![]() 是圆
是圆![]() 的直径.
的直径.
(Ⅱ)解法一:设圆![]() 的圆心为
的圆心为![]() ,则
,则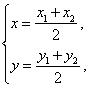
![]() ,
,![]()
又![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
所以圆心的轨迹方程为:![]()
设圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则
![]()
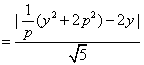
![]()
当![]() 时,
时,![]() 有最小值
有最小值![]() ,由题设得
,由题设得![]()
![]()
![]() ……14分
……14分
解法二:设圆![]() 的圆心为
的圆心为![]() ,则
,则
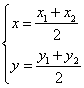
![]()
![]()
又![]()
![]()
![]() …………9分
…………9分
![]()
![]()
![]()
![]()
所以圆心得轨迹方程为![]() …………11分
…………11分
设直线![]() 与
与![]() 的距离为
的距离为![]() ,则
,则![]()
因为![]() 与
与![]() 无公共点.
无公共点.
所以当![]() 与
与![]() 仅有一个公共点时,该点到
仅有一个公共点时,该点到![]() 的距离最小,最小值为
的距离最小,最小值为![]()
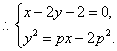
将②代入③![]() ,有
,有
![]() …………14分
…………14分
解法三:设圆![]() 的圆心为
的圆心为![]() ,则
,则
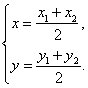
若圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,那么
,那么
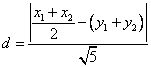
![]()
![]()
又![]()
![]()
![]()
![]()

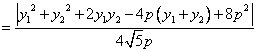
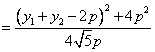
当![]() 时,
时,![]() 有最小值时
有最小值时![]() ,由题设得
,由题设得![]()
![]()


科目:高中数学 来源: 题型:
(06年辽宁卷)(12分)
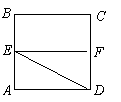
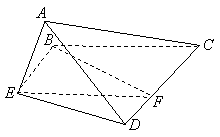
已知正方形![]() ,
,![]() 分别是边
分别是边![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,如图所示,记二面角
折起,如图所示,记二面角![]() 的大小为
的大小为![]() (
(![]() ).
).
(1)证明![]() 平面
平面![]() ;
;
(2)若![]() 为正三角形,试判断点
为正三角形,试判断点![]() 在平面
在平面![]() 内的射影
内的射影![]() 是否在直线
是否在直线![]() 上,证明你的结论,并求角
上,证明你的结论,并求角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(06年辽宁卷文)(12分)
已知函数![]() ,
,![]() ,其中
,其中![]() ,设
,设![]() 为
为![]() 的极小值点,
的极小值点,![]() 为
为![]() 的极值点,
的极值点,![]() ,并且
,并且![]() ,将点
,将点![]() 依次记为
依次记为![]() .
.
(1)求![]() 的值;
的值;
(2)若四边形![]() 为梯形且面积为1,求
为梯形且面积为1,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com