
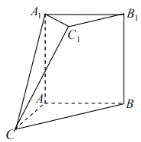
【题目】如图所示的几何体![]() 中,四边形
中,四边形![]() 是正方形,四边形
是正方形,四边形![]() 是梯形,
是梯形,![]() ,且
,且![]() ,
,![]() ,平面
,平面![]() 平面ABC.
平面ABC.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求几何体
,求几何体![]() 的体积.
的体积.
 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆
,过椭圆![]() 的焦点且垂直于
的焦点且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 均在椭圆
均在椭圆![]() 上,点
上,点![]() 在抛物线
在抛物线![]() 上,若
上,若![]() 的重心为坐标原点
的重心为坐标原点![]() ,且
,且![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司![]() 人数众多
人数众多![]() 为鼓励员工利用网络进行营销,准备为员工办理手机流量套餐.为了解员工手机流量使用情况,按照男员工和女员工
为鼓励员工利用网络进行营销,准备为员工办理手机流量套餐.为了解员工手机流量使用情况,按照男员工和女员工![]() 的比例分层抽样,得到
的比例分层抽样,得到![]() 名员工的月使用流量
名员工的月使用流量![]() (单位:
(单位:![]() )的数据,其频率分布直方图如图所示.
)的数据,其频率分布直方图如图所示.
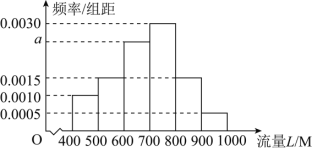
(1)求![]() 的值,并估计这
的值,并估计这![]() 名员工月使用流量的平均值
名员工月使用流量的平均值![]() (同一组中的数据用中点值代表
(同一组中的数据用中点值代表![]() ;
;
(2)若将月使用流量在![]() 以上(含
以上(含![]() )的员工称为“手机营销达人”,填写下面的
)的员工称为“手机营销达人”,填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“成为手机营销达人与员工的性别有关”;
的把握认为“成为手机营销达人与员工的性别有关”;
男员工 | 女员工 | 合计 | |
手机营销达人 | 5 | ||
非手机营销达人 | |||
合计 | 200/span> |
参考公式及数据:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(3)若这![]() 名员工中有
名员工中有![]() 名男员工每月使用流量在
名男员工每月使用流量在![]() ,从每月使用流量在
,从每月使用流量在![]() 的员工中随机抽取名
的员工中随机抽取名![]() 进行问卷调查,记女员工的人数为
进行问卷调查,记女员工的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《高中数学课程标准》(2017版)规定了数学直观想象学科的六大核心素养,为了比较甲、乙两名高二学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图(如图,每项指标值满分为5分,分值高者为优),则下面叙述正确的是(注:雷达图![]() ,又可称为戴布拉图、蜘蛛网图
,又可称为戴布拉图、蜘蛛网图![]() ,可用于对研究对象的多维分析)( )
,可用于对研究对象的多维分析)( )
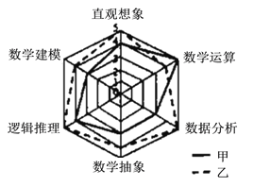
A.甲的直观想象素养高于乙
B.甲的数学建模素养优于数据分析素养
C.乙的数学建模素养与数学运算素养一样
D.乙的六大素养整体水平低于甲
查看答案和解析>>
科目:高中数学 来源: 题型:
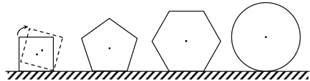
【题目】现有边长均为1的正方形正五边形正六边形及半径为1的圆各一个,在水平桌面上无滑动滚动一周,它们的中心的运动轨迹长分别为![]() ,
,![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】BMI指数(身体质量指数,英文为BodyMassIndex,简称BMI)是衡量人体胖瘦程度的一个标准,BMI=体重(kg)/身高(m)的平方.根据中国肥胖问题工作组标准,当BMI≥28时为肥胖.某地区随机调查了1200名35岁以上成人的身体健康状况,其中有200名高血压患者,被调查者的频率分布直方图如下:
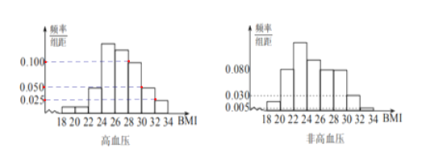
(1)求被调查者中肥胖人群的BMI平均值![]() ;
;
(2)填写下面列联表,并判断是否有99.9%的把握认为35岁以上成人患高血压与肥胖有关.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
肥胖 | 不肥胖 | 合计 | |
高血压 | |||
非高血压 | |||
合计 |
附: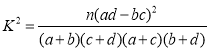 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划投资开发一种新能源产品,预计能获得10万元![]() 1000万元的收益.现准备制定一个对开发科研小组的奖励方案:奖金
1000万元的收益.现准备制定一个对开发科研小组的奖励方案:奖金![]() (单位:万元)随收益
(单位:万元)随收益![]() (单位:万元)的增加而增加,且奖金总数不超过9万元,同时奖金总数不超过收益的
(单位:万元)的增加而增加,且奖金总数不超过9万元,同时奖金总数不超过收益的![]() .
.
(Ⅰ)若建立奖励方案函数模型![]() ,试确定这个函数的定义域、值域和
,试确定这个函数的定义域、值域和![]() 的范围;
的范围;
(Ⅱ)现有两个奖励函数模型:①![]() ;②
;②![]() .试分析这两个函数模型是否符合公司的要求?请说明理由.
.试分析这两个函数模型是否符合公司的要求?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的准线为
的准线为![]() ,其焦点为F,点B是抛物线C上横坐标为
,其焦点为F,点B是抛物线C上横坐标为![]() 的一点,若点B到
的一点,若点B到![]() 的距离等于
的距离等于![]() .
.
(1)求抛物线C的方程,
(2)设A是抛物线C上异于顶点的一点,直线AO交直线![]() 于点M,抛物线C在点A处的切线m交直线
于点M,抛物线C在点A处的切线m交直线![]() 于点N,求证:以点N为圆心,以
于点N,求证:以点N为圆心,以![]() 为半径的圆经过
为半径的圆经过![]() 轴上的两个定点.
轴上的两个定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com