Question

14．三棱柱ABC-A₁B₁C₁的底是边长为1的正三角形，高AA₁=1，在AB上取一点P，设△PA₁C₁与面A₁B₁C₁所成的二面角为α，△PB₁C₁与面A₁B₁C₁所成的二面角为β，则tan（α+β）的最小值是-$\frac{8\sqrt{3}}{13}$．

Answer 1

分析 作PP₁⊥A₁B₁，过P₁作P₁H⊥A₁C₁，由三垂线定理得∠PHP₁=α，设AP=x，求出tanα，同理求出tanβ，由此利用正切加法定理能求出tan（α+β）的最小值．

解答 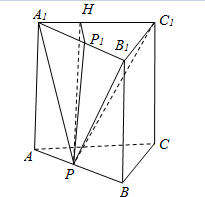解：作PP₁⊥A₁B₁，则PP₁是三棱柱的高．
过P₁作P₁H⊥A₁C₁，连结PH，则∠PHP₁=α，
设AP=x，BP=1-x（0≤x≤1），则$tanα=\frac{2}{{\sqrt{3}x}}$，
同理$tanβ=\frac{2}{{\sqrt{3}（1-x）}}$，
∴$tan（α+β）=\frac{{2\sqrt{3}}}{3x（1-x）-4}≥-\frac{8}{13}\sqrt{3}$（当$x=\frac{1}{2}$时取等号），
∴tan（α+β）的最小值是-$\frac{8\sqrt{3}}{13}$．
故答案为：-$\frac{8\sqrt{3}}{13}$．

点评 本题考查两角和正切的最小值的求法，是中档题，解题时要认真审题，注意三垂线定理和正切加法定理的合理运用．