
如图,在等腰直角△OPQ中,∠POQ=90°,OP=2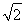 ,点M在线段PQ上.
,点M在线段PQ上.
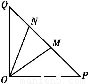
(1)若OM=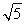 ,求PM的长;
,求PM的长;
(2)若点N在线段MQ上,且∠MON=30°,问:当∠POM取何值时,△OMN的面积最小?并求出面积的最小值.
(1) MP=1或MP=3 (2) ∠POM=30°时,△OMN的面积的最小值为8-4
【解析】
解:(1)在△OMP中,∠OPM=45°,OM= ,OP=2
,OP=2 ,
,
由余弦定理得,OM2=OP2+MP2-2OP·MP·cos45°,
得MP2-4MP+3=0,
解得MP=1或MP=3.
(2)设∠POM=α,0°≤α≤60°,
在△OMP中,由正弦定理,
得 =
= ,
,
所以OM= ,
,
同理ON= .
.
故S△OMN= OM·ON·sin∠MON
OM·ON·sin∠MON
= ×
×
=
=
=
=
=
= .
.
因为0°≤α≤60°,
30°≤2α+30°≤150°,
所以当α=30°时,sin(2α+30°)的最大值为1,
此时△OMN的面积取到最小值.
即∠POM=30°时,△OMN的面积的最小值为8-4 .
.


科目:高中数学 来源: 题型:
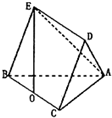 如图,在多面体ABCDE中,底面△ABC为等腰直角三角形,且∠ACB=90°,侧面BCDE是菱形,O点是BC的中点,EO⊥平面ABC.
如图,在多面体ABCDE中,底面△ABC为等腰直角三角形,且∠ACB=90°,侧面BCDE是菱形,O点是BC的中点,EO⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:
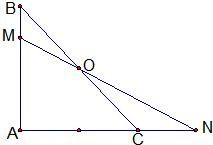 如图在等腰直角△ABC中,点O是斜边BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若
如图在等腰直角△ABC中,点O是斜边BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若| AB |
| AM, |
| AC |
| AN |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
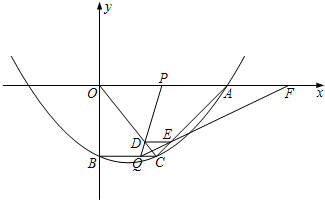 如图,在平面直角坐标系xoy中,抛物线y=
如图,在平面直角坐标系xoy中,抛物线y=| 1 |
| 18 |
| 4 |
| 9 |
| 9 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
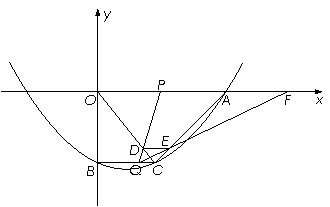
如图,在平面直角坐标系xoy中,抛物线y=![]() x 2-
x 2-![]() x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
(1)求A,B,C三点的坐标和抛物线的顶点坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当t∈(0,![]() )时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
)时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?请写出解答过程.
 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省珠海一中高三(下)第一次调研数学试卷(理科)(解析版) 题型:解答题
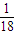 x2-
x2- x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连接AC、现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连接AC、现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒) )时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
)时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;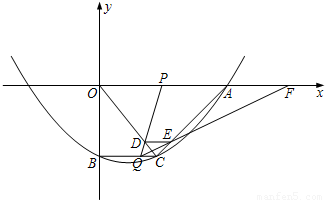
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com