Question

10．如图，正方体ABCD-A₁B₁C₁D₁的棱长为1，P为BC的中点，Q为线段CC₁上的动点，过点A，P，Q的平面截该正方体所得的截面记为S．则下列命题正确的是②④（写出所有正确命题的编号）．
①当0＜CQ＜$\frac{1}{2}$时，S为平行四边形；
②当CQ=$\frac{1}{2}$时，S为等腰梯形；
③当CQ=$\frac{3}{4}$时，S与C₁D₁的交点R满足C₁R=$\frac{1}{4}$
④当CQ=1时，S的面积为$\frac{{\sqrt{6}}}{2}$．

Answer 1

分析 ①当0＜CQ＜$\frac{1}{2}$时，如图所示，PQ∥AM，PQ≠AM，因此截面S为梯形，不是平行四边形，即可判断出正误；
②当CQ=$\frac{1}{2}$时，如图所示，由①可知：截面APQD₁是梯形，利用平行线的性质可得：AP=QD₁，即可判断出S的形状；
③当CQ=$\frac{3}{4}$时，如图所示，AP∩DC=O，点P是BC的中点，可得CO=CD=AB，可得$\frac{{C}_{1}R}{CO}=\frac{{C}_{1}Q}{QC}=\frac{1}{3}$，即可得出C₁R，进而判断出正误．
④当CQ=1时，如图所示，截面S即APC₁E是菱形，对角线长度分别为$\sqrt{3}$，$\sqrt{2}$，即可得出面积．

解答 解：对于①，当0＜CQ＜$\frac{1}{2}$时，如图所示，PQ∥AM，PQ≠AM，因此截面S为梯形，不是平行四边形，故①不正确；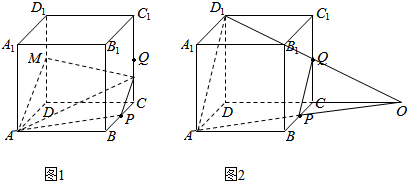

对于②，当CQ=$\frac{1}{2}$时，如图所示，由①可知：截面APQD₁是梯形，利用平行线的性质可得：AP=QD₁，因此可得：S为等腰梯形，故②正确；
对于③，当CQ=$\frac{3}{4}$时，如图所示，AP∩DC=O，∵点P是BC的中点，可得CO=CD=AB，∴$\frac{{C}_{1}R}{CO}=\frac{{C}_{1}Q}{QC}=\frac{1}{3}$，∴S与C₁D₁的交点R满足C₁R=$\frac{1}{3}$，故③不正确；
对于④，当CQ=1时，如图所示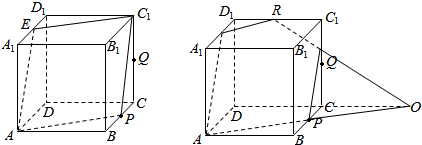，截面S即APC₁E是菱形，对角线长度分别为$\sqrt{3}$，$\sqrt{2}$，
S的面积=$\frac{1}{2}×\sqrt{3}×\sqrt{2}$=$\frac{{\sqrt{6}}}{2}$，故④正确．
故答案为：②④．

点评 本题考查了空间位置关系、平行线的性质、线面平行的判定与性质，考查了空间想象能力、推理能力与计算能力，属于中档题．