
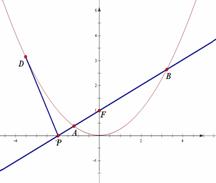
抛物线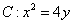 ,直线
,直线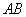 过抛物线
过抛物线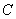 的焦点
的焦点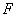 ,交
,交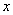 轴于点
轴于点 .
.
(Ⅰ)求证: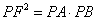 ;
;
(Ⅱ)过 作抛物线
作抛物线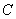 的切线,切点为
的切线,切点为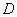 (异于原点),
(异于原点),
(i)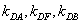 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;
(ii)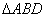 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.
 |
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60o,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
(1)求证:BC⊥平面ACFE;
(2)点M在线段EF上运动,设平面MAB与平面FCB所成二面角的平面角为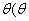 ≤90o),试求cos
≤90o),试求cos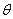 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
甲乙两人进行羽毛球比赛,比赛采取五局三胜制,无论哪一方先胜三局则比赛结束,假定甲每局比赛获胜的概率均为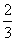 ,则甲以
,则甲以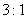 的比分获胜的概率为( )
的比分获胜的概率为( )
A.  B.
B. 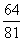 C.
C. 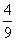 D.
D.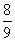
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com