
(1)若g(z)=3,求相应的复数z.
(2)若z=a+bi(a、b∈R)中的a为常数,则令g(z)=f(b),对任意b,是否一定有常数m(m≠0)使得f(b+m)=f(b)?这样的m是否唯一?说明理由.
(3)计算g(2+![]() i),g(-1+
i),g(-1+![]() i),g(1+
i),g(1+![]() i),并设立它们之间的一个等式.
i),并设立它们之间的一个等式.
科目:高中数学 来源: 题型:
A、|z-
| ||
| B、z2=x2-y2 | ||
C、|z-
| ||
| D、|z|≤|x|+|y| |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、|z-
| ||
| B、z2=x2+y2 | ||
C、|z-
| ||
| D、|z|≤|x|+|y| |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京四中高二(下)2月月考数学试卷(理科)(解析版) 题型:选择题
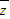 |=2y
|=2y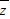 |≥2
|≥2查看答案和解析>>
科目:高中数学 来源:2010年高考数学试卷精编:14.1 复数(解析版) 题型:选择题
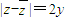
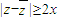
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com