练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设.

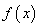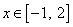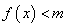    （1）求函数的单调区间；              （2）若当时恒成立，求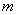的取值范围


    解：（1）由 得或，所以函数的单调增区间为，   单调减区间为

    （2）根据上一步知函数在区间上递增，在区间上递减，在区间上递增，又，所以在区间上，要使恒成立，只需即可


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某兴趣小组测量电视塔AE的高度H(单位：m），如示意图，垂直放置的标杆BC的高度h=4m，仰角∠ABE=，∠ADE=。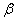

    该小组已经测得一组、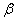的值，tan=1.24，tan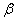=1.20，请据此算出H的值；

    该小组分析若干测得的数据后，认为适当调整标杆到电视塔的距离d（单位：m），使与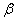之差较大，可以提高测量精确度。若电视塔的实际高度为125m，试问d为多少时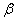，-最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列的前n项和（n为正整数）。

    （Ⅰ）令，求证数列是等差数列，并求数列的通项公式；

    (Ⅱ）令，，求。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    正方体中，二面角的正切值为 （     ）

    A．               B．           C．            D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若，计算积分   dx=_____________

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数,则的值为（　　）                                                  

        A．2    B．3  C．4    D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列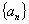满足，给出下列命题：

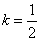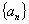    ①当时，数列为递减数列

    ②当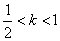时，数列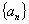不一定有最大项

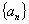    ③当时，数列为递减数列

    ④当为正整数时，数列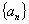必有两项相等的最大项

    其中真命题的个数为（    ）

    A．0        B．1      C．2          D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某几何体的三视图如图所示，则该几何体中，面积最大的侧面的面积为（　　）

    A．             B．      

    C．             D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在已知函数f(x)＝Asin (ωx＋φ)，x∈R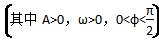的图象与x轴的交点中，相邻两个交点之间的距离为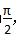，且图象上一个最低点为M．

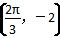    (1)求f(x)的解析式；

    (2)当x∈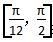时，求f(x)的值域．

    查看答案和解析>>

    同步练习册答案