
已知三棱锥S﹣ABC,满足SA⊥SB,SB⊥SC,SC⊥SA,且SA=SB=SC,若该三棱锥外接球的半径为 ,Q是外接球上一动点,则点Q到平面ABC的距离的最大值为( )
,Q是外接球上一动点,则点Q到平面ABC的距离的最大值为( )
A.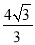 B.
B. C.3 D.2
C.3 D.2
科目:高中数学 来源:2015-2016学年福建福州五校高二下期中文科数学试卷(解析版) 题型:解答题
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品.从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:
甲厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14] |
频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
乙厂:
分组 | [ 29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14] |
频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由于以上统计数据填下面 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
甲 厂 | 乙 厂 | 合计 | |
优质品 | |||
非优质品 | |||
合计 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省高二下期中理科数学B卷(解析版) 题型:解答题
如图,已知四棱锥的侧棱PD⊥底面ABCD,且底面ABCD是直角梯形,AD⊥CD,AB∥CD,AB=AD= CD=2,点M在侧棱上.
CD=2,点M在侧棱上.

(1)求证:BC⊥平面BDP;
(2)若侧棱PC与底面ABCD所成角的正切值为 ,点M为侧棱PC的中点,求异面直线BM与PA所成角的余弦值.
,点M为侧棱PC的中点,求异面直线BM与PA所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省高二下期中理科数学B卷(解析版) 题型:选择题
设平面向量 、
、 满足|
满足| |=2、|
|=2、| |=1,
|=1, ,点P满足
,点P满足 ,则点P所表示的轨迹长度为( )
,则点P所表示的轨迹长度为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省高二下期中理科数学B卷(解析版) 题型:选择题
设复数 其中a为实数,若z的实部为2,则z的虚部为( )
其中a为实数,若z的实部为2,则z的虚部为( )
A.- B.-
B.- i C.-
i C.- D.-
D.- i
i
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省高二下期中理科数学A卷(解析版) 题型:解答题
如图,已知四棱锥的侧棱PD⊥底面ABCD,且底面ABCD是直角梯形,AD⊥CD,AB∥CD,AB=AD= CD=2,点M在侧棱上.
CD=2,点M在侧棱上.

(1)求证:BC⊥平面BDP;
(2)若侧棱PC与底面ABCD所成角的正切值为 ,点M为侧棱PC的中点,求异面直线BM与PA所成角的余弦值.
,点M为侧棱PC的中点,求异面直线BM与PA所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省高二下期中理科数学A卷(解析版) 题型:选择题
设复数 其中a为实数,若z的实部为2,则z的虚部为( )
其中a为实数,若z的实部为2,则z的虚部为( )
A.- B.-
B.- i C.-
i C.- D.-
D.- i
i
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com