练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(x)=a(x+2a)(x-a-3),g(x)=2-x-2,同时满足以下两个条件:

    ①∀x∈R,f(x)<0或g(x)<0;②∃x0∈(1,+∞),f(x0)g(x0)<0成立,则实

    数a的取值范围是　　　　　.

    -4<a<-2或-<a<0【解题提示】首先由g(x)<0求出x的取值范围,然后结合图象列不等式组求解.

    【解析】由已知f(x)=a(x+2a)(x-a-3),g(x)=2-x-2,根据①∀x∈R,f(x)<0或g(x)<0,即函数f(x)和函数g(x)不能同时取非负值,由g(x)<0,求得x>-1,即当x>-1时,g(x)<0;

    当x≤-1时,g(x)≥0,故当x≤-1时,f(x)<0.根据②∃x0∈(1,+∞),f(x0)g(x0)<0成立,而当x0>1时,g(x0)=-2<0,故f(x0)=a(x0+2a)(x0-a-3)>0在(1,+∞)上有解,即当x>1时,函数f(x)在x轴的上方有图象,故有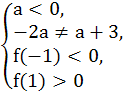

    解得:-4<a<-2或-<a<0.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知f(x)=2cos(ωx+θ)，(x∈R，0≤θ≤
    π
    2
    )    ，g（x）=ex-x2+2ax-1，（x∈R，a为实数），y=f（x）的图象与y轴交于点(0，
    		3
    )    ，且在该点处切线的斜率为-2．
    （I）若点A(
    π
    2
    ，0)    ，点P是函数y=f（x）图象上一点，Q（x0，y0）是PA的中点，当y0=
    		3
    2
    ，x0∈[
    π
    2
    ，π]    时，求x0的值；
    （II）当a＞1+ln2时，试问：是否存在曲线y=f（x）与y=g（x）的公切线？并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（x）在实数集上是减函数，若a+b≤0，则下列正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(x)=
    a(x-1)2
    2x+b
    ，曲线y=f(x)    与直线l：4x+3y-5=0切于点A的横坐标为2，g(x)=2x-
    1
    3
    ．
    （1）求函数f（x）的解析式；
    （2）求函数f（x）的单调区间；
    （3）若对于一切x∈[2，5]，总存在x1∈[m，n]，使f（x）=g（x1）成立，求n-m的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（x）的定义域是x≠0的一切实数，对于定义域内任意的x1，x2都有f（x1•x2）=f（x1）+f（x2），且当x＞1时，f（x）＞0，f（2）=1．
    （1）求证f（x）是偶函数；
    （2）求证f（x）在（0，+∞）上是增函数；
    （3）若f（a+1）＞f（a）+1，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（x）是定义在（0，+∞）上的函数，且对任意正数x，y都有f（xy）=f（x）+f（y），且当x＞1时，f（x）＞0．
    （1）证明f（x）在（0，+∞）上为增函数；
    （2）若f（3）=1，集合A={x|f（x）＞f（x-1）+2}，B={x|f(
    (a+1)x-1x+1
    )＞0，a∈R}    ，A∩B=∅，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案