
【题目】某医院体检中心为回馈大众,推出优惠活动:对首次参加体检的人员,按200元次收费,并注册成为会员,对会员的后续体检给予相应优惠,标准如下:
体检次序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次及以上 |
收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.8 |
该体检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计,得到数据如下表:
体检次数 | 一次 | 两次 | 三次 | 四次 | 五次及以上 |
频数 | 60 | 20 | 10 | 5 | 5 |
假设该体检中心为顾客体检一次的成本费用为150元,根据所给数据,解答下列问题:
(1)该体检中心要从这100人里至少体检3次的会员中,按体检次数用分层抽样的方法抽出8人,再从这8人中抽出2人发放纪念品,求抽出的2人中恰有1人体检3次的概率;
(2)若以这100位会员体检次数的频率分布估计该体检中心所有会员体检次数的概率分布,已知该中心本周共接待了1000名顾客参加体检,试估计该体检中心本周所获利润.
【答案】(1)![]() (2)42500元
(2)42500元
【解析】
(1)根据分层抽样计算出抽出的![]() 人中有
人中有![]() 人体检三次,有
人体检三次,有![]() 人体检四次,有
人体检四次,有![]() 人体检五次及以上.,用组合知识求出从8人中抽取2人的方法数,以及有1 人体检3次的方法数,然后计算概率;
人体检五次及以上.,用组合知识求出从8人中抽取2人的方法数,以及有1 人体检3次的方法数,然后计算概率;
(2)按比例估算出参数体检一次、二次、三次、四次、五次及以上的人数后可计算出利润.
解:(1)由题,抽出的![]() 人中有
人中有![]() 人体检三次,有
人体检三次,有![]() 人体检四次,有
人体检四次,有![]() 人体检五次及以上.
人体检五次及以上.
从![]() 个人中抽取两人共有
个人中抽取两人共有![]() 种取法,其中恰有
种取法,其中恰有![]() 人体检
人体检![]() 次的情况有
次的情况有![]() 种,
种,
![]() 所求概率为
所求概率为![]() ;
;
(2)由题可估计:这![]() 名顾客中,在体检中心参加的本次体检是他在此中心参加的第一次体检的有
名顾客中,在体检中心参加的本次体检是他在此中心参加的第一次体检的有![]() 人,
人,
第二次体检的有![]() 人,第三次体检的有
人,第三次体检的有![]() 人,
人,
第四次体检的有![]() 人,第五次及五次以上体检的有
人,第五次及五次以上体检的有![]() 人,
人,
![]() 医院的收入约为
医院的收入约为
![]()
又医院成本为![]() ,
,
![]() 利润为
利润为![]() 元.
元.


科目:高中数学 来源: 题型:
【题目】已知圆锥的顶点为![]() ,底面圆
,底面圆![]() 的两条直径分别为
的两条直径分别为![]() 和
和![]() ,且
,且![]() ,若平面
,若平面![]() 平面
平面![]() .现有以下四个结论:
.现有以下四个结论:
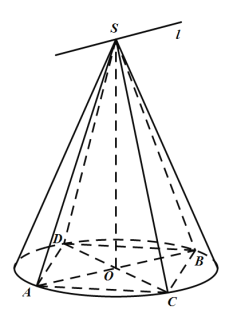
①![]() 平面
平面![]() ;
;
②![]() ;
;
③若![]() 是底面圆周上的动点,则
是底面圆周上的动点,则![]() 的最大面积等于
的最大面积等于![]() 的面积;
的面积;
④![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代典籍《周易》用“卦”描述万物的变化,每一卦由六爻组成.其中有一种起卦方法称为“金钱起卦法”,其做法为:取三枚相同的钱币合于双手中,上下摇动数下使钱币翻滚摩擦,再随意抛撒钱币到桌面或平盘等硬物上,如此重复六次,得到六爻.若三枚钱币全部正面向上或全部反面向上,就称为变爻.若每一枚钱币正面向上的概率为![]() ,则一卦中恰有两个变爻的概率为( )
,则一卦中恰有两个变爻的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国的嫦娥四号探测器,简称“四号星”,是世界首个在月球背面软着陆和巡视探测的航天器.2019年9月25日,中国科研人员利用嫦娥四号数据精确定位了嫦娥四号的着陆位置,并再现了嫦娥四号的落月过程,该成果由国际科学期刊《自然·通讯》在线发表.如图所示,

现假设“四号星”沿地月转移轨道飞向月球后,在月球附近一点![]() 变轨进入以月球球心
变轨进入以月球球心![]() 为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在
为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在![]() 点第二次变轨进入仍以
点第二次变轨进入仍以![]() 为一个焦点的椭圆轨道Ⅱ绕月飞行.若用
为一个焦点的椭圆轨道Ⅱ绕月飞行.若用![]() 和
和![]() 分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用
分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用![]() 和
和![]() 分别表示椭圆轨道Ⅰ和Ⅱ的长轴长,给出下列式子:①
分别表示椭圆轨道Ⅰ和Ⅱ的长轴长,给出下列式子:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的式子的序号是( )
.其中正确的式子的序号是( )
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十三届全国人大二次会议于2019年3月5日在京召开为了了解某校大学生对两会的关注程度,学校媒体在开幕后的第二天,从全校学生中随机抽取了180人,对是否收看2019年两会开幕会情况进行了问卷调查,统计数据如下:
收看 | 没收看 | |
男生 | 80 | 40 |
女生 | 30 | 30 |
(1)根据上表说明,在犯错误的概率不超过1%的前提下,能否认为该校大学生收看开幕会与性别有关?(计算结果精确到0.001)
(2)现从随机抽取的学生中,采用按性别分层抽样的方法选取6人,来参加2019年两会的志愿者宣传活动,若从这6人中随机选取2人到各班级宣传介绍,求恰好选到一名男生和一名女生的概率. 附 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记无穷数列![]() 的前n项
的前n项![]() ,
,![]() ,…,
,…,![]() 的最大项为
的最大项为![]() ,第n项之后的各项
,第n项之后的各项![]() ,
,![]() ,…的最小项为
,…的最小项为![]() ,
,![]() .
.
(1)若数列![]() 的通项公式为
的通项公式为![]() ,写出
,写出![]() ,
,![]() ,并求数列
,并求数列![]() 通项公式;
通项公式;
(2)若数列![]() 的通项公式为
的通项公式为![]() ,判断
,判断![]() 是否为等差数列,若是,求出公差;若不是,请说明理由;
是否为等差数列,若是,求出公差;若不是,请说明理由;
(3)若数列![]() 为公差大于零的等差数列,求证:
为公差大于零的等差数列,求证:![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解全市统考情况,从所有参加考试的考生中抽取4000名考生的成绩,频率分布直方图如下图所示.

(1)求这4000名考生的半均成绩![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)由直方图可认为考生考试成绩z服从正态分布![]() ,其中
,其中![]() 分别取考生的平均成绩
分别取考生的平均成绩![]() 和考生成绩的方差
和考生成绩的方差![]() ,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
(3)如果用抽取的考生成绩的情况来估计全市考生的成绩情况,现从全市考生中随机抽取4名考生,记成绩不超过84.81分的考生人数为![]() ,求
,求![]() .(精确到0.001)
.(精确到0.001)
附:①![]() ;
;
②![]() ,则
,则![]() ;
;
③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济全球化、信息化的发展,企业之间的竞争从资源的争夺转向人才的竞争,吸引、留住培养和用好人才成为人力资源管理的战略目标和紧迫任务,在此背景下,某信息网站在15个城市中对刚毕业的大学生的月平均收入薪资和月平均期望薪资做了调查,数据如下图所示.
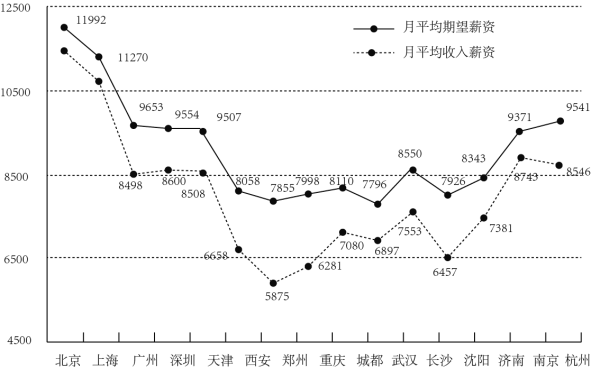
(1)若某大学毕业生从这15座城市中随机选择一座城市就业,求该生选中月平均收入薪资高于8500元的城市的概率;
(2)现有2名大学毕业生在这15座城市中各随机选择一座城市就业,且2人的选择相互独立,记X为选中月平均收入薪资高于8500元的城市的人数,求X的分布列和数学期望E(X);
(3)记图中月平均收入薪资对应数据的方差为![]() ,月平均期望薪资对应数据的方差为
,月平均期望薪资对应数据的方差为![]() ,判断
,判断![]() 与
与![]() 的大小(只需写出结论)
的大小(只需写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com