
【题目】已知函数![]() ,
,![]() .
.
(1)若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(2)证明:![]() .
.
(3)设方程![]() 的实根为
的实根为![]() .令
.令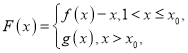 若存在
若存在![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() (2)证明见解析(3)证明见解析
(2)证明见解析(3)证明见解析
【解析】
(1)由题意可得,![]() ,令
,令![]() ,利用导数得
,利用导数得![]() 在
在![]() 上单调递减,进而可得结论;
上单调递减,进而可得结论;
(2)不等式转化为![]() ,令
,令![]() ,
,![]() ,利用导数得单调性即可得到答案;
,利用导数得单调性即可得到答案;
(3)由题意可得![]() ,进而可将不等式转化为
,进而可将不等式转化为![]() ,再利用单调性可得
,再利用单调性可得![]() ,记
,记![]() ,
,![]() ,再利用导数研究单调性可得
,再利用导数研究单调性可得![]() 在
在![]() 上单调递增,即
上单调递增,即![]() ,即
,即![]() ,即可得到结论.
,即可得到结论.
(1)![]() ,即
,即![]() ,化简可得
,化简可得![]() .
.
令![]() ,
,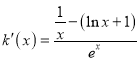 ,因为
,因为![]() ,所以
,所以![]() ,
,![]() .
.
所以![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,![]() .
.
所以![]() 的最小值为
的最小值为![]() .
.
(2)要证![]() ,即
,即![]() .
.
两边同除以![]() 可得
可得![]() .
.
设![]() ,则
,则![]() .
.
在![]() 上,
上,![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
在![]() 上,
上,![]() ,所以
,所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() .
.
设![]() ,因为
,因为![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() .
.
所以![]() ,即
,即![]() .
.
(3)证明:方程![]() 在区间
在区间![]() 上的实根为
上的实根为![]() ,即
,即![]() ,要证
,要证
![]() ,由
,由![]() 可知,即要证
可知,即要证![]() .
.
当![]() 时,
时,![]() ,
,![]() ,因而
,因而![]() 在
在![]() 上单调递增.
上单调递增.
当![]() 时,
时,![]() ,
,![]() ,因而
,因而![]() 在
在![]() 上单调递减.
上单调递减.
因为![]() ,所以
,所以![]() ,要证
,要证![]() .
.
即要证![]() .
.
记![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() ,则
,则![]() .
.
![]() .
.
设![]() ,
,![]() ,当
,当![]() 时,
时,![]() .
.
![]() 时,
时,![]() ,故
,故![]() .
.
且![]() ,故
,故![]() ,因为
,因为![]() ,所以
,所以![]() .
.
因此![]() ,即
,即![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() ,即
,即![]() .
.
故![]() 得证.
得证.


科目:高中数学 来源: 题型:
【题目】某医院体检中心为回馈大众,推出优惠活动:对首次参加体检的人员,按200元次收费,并注册成为会员,对会员的后续体检给予相应优惠,标准如下:
体检次序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次及以上 |
收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.8 |
该体检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计,得到数据如下表:
体检次数 | 一次 | 两次 | 三次 | 四次 | 五次及以上 |
频数 | 60 | 20 | 10 | 5 | 5 |
假设该体检中心为顾客体检一次的成本费用为150元,根据所给数据,解答下列问题:
(1)该体检中心要从这100人里至少体检3次的会员中,按体检次数用分层抽样的方法抽出8人,再从这8人中抽出2人发放纪念品,求抽出的2人中恰有1人体检3次的概率;
(2)若以这100位会员体检次数的频率分布估计该体检中心所有会员体检次数的概率分布,已知该中心本周共接待了1000名顾客参加体检,试估计该体检中心本周所获利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,
上,![]() 平面
平面![]() ,
,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
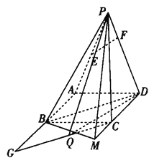
(1)证明:![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() 的平行线,与直线
的平行线,与直线![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 的中点,求
的中点,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形![]() 中,
中,![]() ,
,![]() ,现将长方形沿对角线
,现将长方形沿对角线![]() 折起,使
折起,使![]() ,得到一个四面体
,得到一个四面体![]() ,如图所示.
,如图所示.
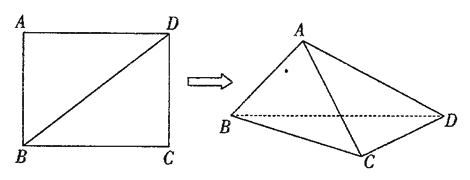
(1)试问:在折叠的过程中,异面直线![]() 与
与![]() 能否垂直?若能垂直,求出相应的
能否垂直?若能垂直,求出相应的![]() 的值;若不垂直,请说明理由;
的值;若不垂直,请说明理由;
(2)当四面体![]() 体积最大时,求二面角
体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,
的球面上,![]() 是面积为
是面积为![]() 的等边三角形,
的等边三角形,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
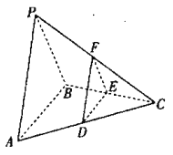
(1)确定![]() 的位置(需要说明理由),并证明:平面
的位置(需要说明理由),并证明:平面![]() 平面
平面![]() .
.
(2)与侧面![]() 平行的平面
平行的平面![]() 与棱
与棱![]() ,
,![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,
,![]() ,求四面体
,求四面体![]() 的体积的最大值.
的体积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com