
设M是弧度为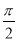 的∠AOB的角平分线上的一点,且OM=1,过M任作一直线与∠AOB的两边分别交OA、OB于点E,F,记∠OEM=x.
的∠AOB的角平分线上的一点,且OM=1,过M任作一直线与∠AOB的两边分别交OA、OB于点E,F,记∠OEM=x.
(1)若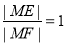 时,试问x的值为多少?(2)求
时,试问x的值为多少?(2)求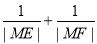 的取值范围.
的取值范围.
(1)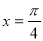 ,(2)
,(2)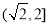 .
.
【解析】
试题分析: (1)如图,当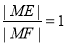 时,即M为EF的中点,又M是∠AOB的角平分线上的一点,由几何性质易知
时,即M为EF的中点,又M是∠AOB的角平分线上的一点,由几何性质易知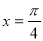 ,(2)由已知条件,在三角形OEM与三角形OFM中,根据正弦定理可求得
,(2)由已知条件,在三角形OEM与三角形OFM中,根据正弦定理可求得 与
与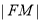 关于x的函数关系,从而得到
关于x的函数关系,从而得到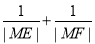 与x的函数关系,利用三角函数知识即可求
与x的函数关系,利用三角函数知识即可求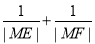 的取值范围,但要注意x的范围限制.
的取值范围,但要注意x的范围限制.
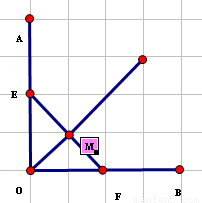
试题解析:(1)当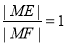 时,即M为EF的中点,又M是∠AOB的角平分线上的一点,由几何性质可知OM为∠AOB 的对称轴,则E与F点关于OM对称,所以
时,即M为EF的中点,又M是∠AOB的角平分线上的一点,由几何性质可知OM为∠AOB 的对称轴,则E与F点关于OM对称,所以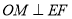 ,在
,在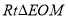 中,
中,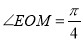 ,所以
,所以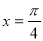 .(2)在三角形OEM中由正弦定理可知:
.(2)在三角形OEM中由正弦定理可知: ,
,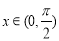 ,同理在三角形OFM中由正弦定理可知:
,同理在三角形OFM中由正弦定理可知: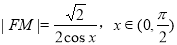 ,从而
,从而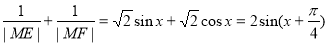 ,∴
,∴ ∴
∴ ,即有
,即有 ,故
,故 .
.
考点:正弦定理,归一公式,给定自变量范围的三角函数求值域问题,函数的思想.


科目:高中数学 来源:2016届江西省高一下学期第二次段考数学试卷(解析版) 题型:填空题
下列命题中:①不等式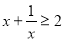 恒成立;②在三角形ABC中,如果有sinA=sinB成立,则必有A=B;③将两个变量所对应的点在平面直角坐标系中描出来,如果所描的点在散点图中没有显示任何关系则称变量间是不相关的;④等差数列{an}的首项a1=-50,公差d=2,前n项和为Sn,则n=25或n=26是使Sn取到最大值;其中为正确命题的序号是: .
恒成立;②在三角形ABC中,如果有sinA=sinB成立,则必有A=B;③将两个变量所对应的点在平面直角坐标系中描出来,如果所描的点在散点图中没有显示任何关系则称变量间是不相关的;④等差数列{an}的首项a1=-50,公差d=2,前n项和为Sn,则n=25或n=26是使Sn取到最大值;其中为正确命题的序号是: .
查看答案和解析>>
科目:高中数学 来源:2016届江西省高一下学期第二次段考数学试卷(解析版) 题型:选择题
在△ABC中,内角A、B、C的对边分别是a,b,c,若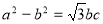 ,
,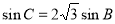 ,则A=( ).
,则A=( ).
A.30° B.60° C.120° D.150°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com