
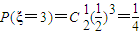 ,
,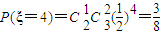 ,
,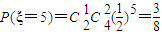 ,由此能求出ξ的数学期望.
,由此能求出ξ的数学期望.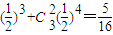
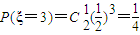
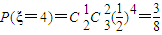
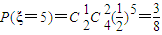
| ξ | 3 | 4 | 5 |
| P |  |  |  |
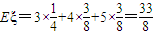 .
.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年衡阳八中文)(12分)
为丰富学生的课余生活,学校决定在高一年段开设系列选修课,并开放了三间多媒体教室,且各门选修课是否使用多媒体教室互不影响.
(1)若周一下午开设的A、B、C三门选修课使用多媒体教室的概率分别为![]() 求这三门选修课中恰有二门课使用多媒体教室的概率;
求这三门选修课中恰有二门课使用多媒体教室的概率;
(2)若周二下午开设的五门选修课使用多媒体教室的概率均为![]() ,求多媒体教室不够使用的概率.
,求多媒体教室不够使用的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算其数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
(文)为丰富学生的课余生活,学校决定在高一年级开设系列选修课,并开放了三间多媒体教室,且各门选修课是否使用多媒体教室互不影响.
(1)若周一下午开设的A、B、C三门选修课使用多媒体教室的概率分别为![]() 、
、![]() 、
、![]() ,求这三门选修课中恰有两门课使用多媒体教室的概率;
,求这三门选修课中恰有两门课使用多媒体教室的概率;
(2)若周二下午开设的五门选修课使用多媒体教室的概率均为![]() ,求多媒体教室不够用的概率.
,求多媒体教室不够用的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com