
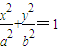 (a>b>0)的离心率为
(a>b>0)的离心率为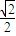 ,不等式
,不等式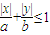 所表示的平面区域的面积为
所表示的平面区域的面积为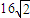 .
.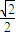 ,可得a=
,可得a=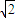 b,根据不等式
b,根据不等式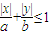 所表示的平面区域的面积为
所表示的平面区域的面积为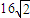 ,可得
,可得 ,由此可求得a,b的值,从而可得椭圆C的方程;
,由此可求得a,b的值,从而可得椭圆C的方程;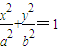 (a>b>0)的离心率为
(a>b>0)的离心率为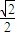 ,∴
,∴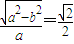
 b①
b①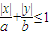 所表示的平面区域是椭圆C的四个顶点为顶点的菱形
所表示的平面区域是椭圆C的四个顶点为顶点的菱形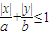 所表示的平面区域的面积为
所表示的平面区域的面积为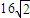 .
.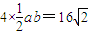 ②
②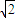
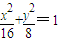 ;
;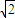 ),可得AB的垂直平分线L的方程为:
),可得AB的垂直平分线L的方程为: =0
=0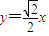
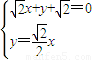 得x=-
得x=- ,y=-
,y=-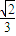
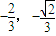 ),此时
),此时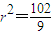
 .
.

 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| |OP| |
| |OM| |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| |x| |
| a |
| |y| |
| b |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| |x| |
| a |
| |y| |
| b |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com