Question

（08年内江市三模） (12分) 如图，已知平面，平面，三角形为等边三角形，

，为的中点

（1）求证：平面；

（2）求证：平面平面；

（3）求二面角的大小。

 

 

 

Answer 1

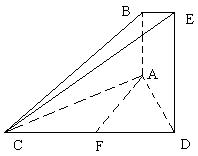
解析：（1）证明：取的中点，连，

∵为的中点 

∴，而平面，平面，

故，又，

∴四边形为平行四边形

∴      ……………………………………. 2分

所以平面      ……………………………………. 3分

（2）∵为等边三角形，∴，而

故平面      ……………………………………. 5分

∵，∴平面

所以平面平面      ……………………. 7分

（3）在平面内作交于，在平面内作交于，连  ∵平面平面  ∴平面，由三垂线定理得

∴为二面角的平面角      ……………………………………. 9分

设，则，

∴      …… 10分

又，其中  ∴     …11分

∴

所以二面角的大小为（或）      ………. 12分

方法二：

设，则；由已知得

建立如图所示的坐标系，      ………………………………. 1分

则：

∵为的中点，∴      ………2分

（1）证明：      ………3分

∵，A不在平面内，∴平面      ………… 4分

（2）∵   ……………. 5分

∴，∴      ………………………6分

∴平面，又平面

∴平面平面      ………………………………. 7分

（3）设平面的法向量为

由可得：      ……………………………. 8分

设平面的法向量为

由可得：      …………………………9分

∴      ………………………………. 11分

∴二面角的大小为      ………………………………. 12分