
| ÖÜŅ» | ĪŽÓź | ĪŽÓź | ÓŠÓź | ÓŠÓź |
| Öܶž | ĪŽÓź | ÓŠÓź | ĪŽÓź | ÓŠÓź |
| ŹÕŅę | 20Ķņ | 15Ķņ | 10Ķņ | 7.5Ķņ |
·ÖĪö £Ø1£©½āÉčĻĀÖÜŅ»ÓŠÓźµÄøÅĀŹĪŖp£¬ÓÉĢāŅā£¬p2=0.36£¬p=0.6£¬»łµŲŹÕŅęxµÄæÉÄÜȔֵĪŖ20£¬15£¬10£¬7.5£¬·Ö±šĒó³öĻąÓ¦µÄøÅĀŹ£¬ÓÉ“ĖÄÜĒó³ö»łµŲŹÕŅęXµÄ·Ö²¼ĮŠŗĶ»łµŲµÄŌ¤ĘŚŹÕŅę£®
£Ø2£©É軳µŲ¶īĶāĘøĒė¹¤ČĖŹ±µÄŹÕŅęĪŖYĶņŌŖ£¬ĘäŌ¤ĘŚŹÕŅęE£ØY£©=16-a£ØĶņŌŖ£©£¬E£ØY£©-E£ØX£©=1.6-a£¬ÓÉ“ĖÄÜĒó³ö½į¹ū£®
½ā“š ½ā£ŗ£Ø1£©ÉčĻĀÖÜŅ»ÓŠÓźµÄøÅĀŹĪŖp£¬
ÓÉĢāŅā£¬p2=0.36£¬p=0.6£¬»łµŲŹÕŅęxµÄæÉÄÜȔֵĪŖ20£¬15£¬10£¬7.5£¬
ŌņP£ØX=20£©=0.36£¬
P£ØX=15£©=0.24£¬
P£ØX=10£©=0.24£¬
P£ØX=7.5£©=0.16£¬
ĖłŅŌ»łµŲŹÕŅęXµÄ·Ö²¼ĮŠĪŖ£ŗ
| X | 20 | 15 | 10 | 7.5 |
| P | 0.36 | 0.24 | 0.24 | 0.16 |
µćĘĄ ±¾Ģāæ¼²éĄėÉ¢ŠĶĖ껜±äĮæµÄŹżŃ§ĘŚĶūµÄĒó·ØÓėÓ¦ÓĆ£¬ŹĒÖŠµµĢā£¬½āĢāŹ±ŅŖČĻÕęÉóĢā£¬ŌŚĄśÄźøßæ¼ÖŠ¶¼ŹĒ±Ųæ¼ÖŖŹ¶µćÖ®Ņ»£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | a=$\frac{1}{2}$ | B£® | a=$\frac{1}{2}$»ņa=0 | C£® | a=0 | D£® | a”Ü$\frac{1}{2}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -$\frac{\sqrt{1-{t}^{2}}}{t}$ | B£® | $\frac{\sqrt{1-{t}^{2}}}{t}$ | C£® | $\frac{\sqrt{1+{t}^{2}}}{t}$ | D£® | -$\frac{\sqrt{1+{t}^{2}}}{t}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
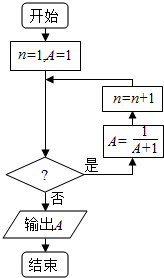 ŅŃÖŖŹżĮŠ{an}ÖŠ£¬${a_1}=1£¬{a_{n+1}}=\frac{1}{{1+{a_n}}}$£¬ČōĄūÓĆĻĀĆę³ĢŠņæņĶ¼¼ĘĖćøĆŹżĮŠµÄµŚ2016Ļī£¬ŌņÅŠ¶ĻæņÄŚµÄĢõ¼žŹĒ£Ø””””£©
ŅŃÖŖŹżĮŠ{an}ÖŠ£¬${a_1}=1£¬{a_{n+1}}=\frac{1}{{1+{a_n}}}$£¬ČōĄūÓĆĻĀĆę³ĢŠņæņĶ¼¼ĘĖćøĆŹżĮŠµÄµŚ2016Ļī£¬ŌņÅŠ¶ĻæņÄŚµÄĢõ¼žŹĒ£Ø””””£©| A£® | n”Ü2014 | B£® | n”Ü2016 | C£® | n”Ü2015 | D£® | n”Ü2017 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -2 | B£® | 0 | C£® | $\frac{2}{3}$ | D£® | 2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
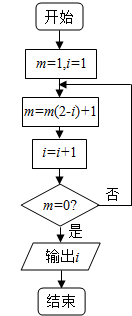
| A£® | 3 | B£® | 4 | C£® | 5 | D£® | 6 |
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com