
分析 (1)由圆的方程可得圆心坐标为($\frac{2-m}{2}$,$\frac{-m-1}{2}$),半径r=$\frac{1}{2}$$\sqrt{2{m}^{2}-6m+13}$,由二次函数的最值可得;
(2)可得距离d=$\frac{1}{2}$$\sqrt{2{m}^{2}-2m+5}$,由二次函数可得.
解答 解:(1)∵圆C的方程为x2+y2+(m-2)x+(m+1)y+m-2=0,
∴圆心坐标为($\frac{2-m}{2}$,$\frac{-m-1}{2}$),
半径r=$\frac{1}{2}$$\sqrt{(m-2)^{2}+(m+1)^{2}-4(m-2)}$=$\frac{1}{2}$$\sqrt{2{m}^{2}-6m+13}$
由开口向上的二次函数的性质知当m=-$\frac{-6}{2×2}$=$\frac{3}{2}$时,半径取最小值$\frac{\sqrt{34}}{4}$,圆的面积最小,
此时圆心为($\frac{1}{4}$,-$\frac{5}{4}$),半径r=$\frac{\sqrt{34}}{4}$;
(2)由(1)圆心与原点的距离d=$\sqrt{(\frac{2-m}{2})^{2}+(\frac{-m-1}{2})^{2}}$=$\frac{1}{2}$$\sqrt{2{m}^{2}-2m+5}$,
由二次函数知当m=-$\frac{-2}{2×2}$=$\frac{1}{2}$时,圆心距离坐标原点最近,
此时圆心为($\frac{3}{4}$,-$\frac{3}{4}$),半径r=$\frac{\sqrt{42}}{4}$
点评 本题考查圆的一般式方程,涉及二次函数的最值,属中档题.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x}$ | B. | y=-sinx | C. | y=-lnx | D. | y=lg($\sqrt{{x}^{2}+1}$-x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 标准差 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
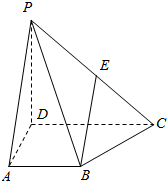 四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,AD⊥DC,侧棱PD⊥底面ABCD,且AB=AD=1,PD=DC=2,E是PC的中点.
四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,AD⊥DC,侧棱PD⊥底面ABCD,且AB=AD=1,PD=DC=2,E是PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com