
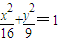 上的一个动点,则x+y的最大值是 .
上的一个动点,则x+y的最大值是 .  怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
|
| OM |
| 1 |
| 2 |
| ON |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年长沙一中一模理)(13分)已知函数f (x) = lnx,g (x) =![]() (a>0),设F(x) = f (x) + g (x).
(a>0),设F(x) = f (x) + g (x).
![]() (1)求函数F(x)的单调区间;
(1)求函数F(x)的单调区间;
(2)若点![]() 为函数
为函数![]() 的图象上任意一点,当
的图象上任意一点,当![]() 时,点P处的切线的斜率k≤
时,点P处的切线的斜率k≤![]() 恒成立,求实数a的最小值;
恒成立,求实数a的最小值;
(3)是否存在实数m,使得函数y = g(![]() ) + m 1的图象与函数y = f (1 + x2)的图象恰有四个不同的交点?若存在,求出实数m的取值范围;若不存在,说明理由.
) + m 1的图象与函数y = f (1 + x2)的图象恰有四个不同的交点?若存在,求出实数m的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年周至二中四模理) 已知曲线f(x)=x3+x2+x+3在x= -1处的切线恰好与抛物线y=2px2相切,则过该抛物线的焦点且垂直于对称轴的直线与抛物线相交得的线段长度为 ( )
A.4 B.![]() C.8 D.
C.8 D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com