当n∈N+时,定义函数N(n)表示n的最大奇因数.如N(1)=1,N(2)=1,N(3)=3,N(4)=1,N(5)=5,N(10)=5,记S(n)=N(2n-1)+N(2n-1+1)+…+N(2n-1)(n∈R+)则:(1)S(3)=________;(2)S(n)=________.
解:因N(2
n)=1,
当n为奇数时,N(n)=n,
在从2
n-1到2
n-1这2
n-1个数中,奇数有2
n-2个,偶数有2
n-2个.
在这2
n-2个偶数中,不同的偶数的最大奇因数一定不同,
从2
n-1到2
n-1共有2
n-1个数,而1到2
n-1共有2
n-1个不同的奇数,
故有N(2
n-1)=2
1-1=1,N(2
n-1+1)=2
2-1=3,…,N(2
n-1)=2
n-1.
那么S(n)=N(2
n-1)+N(2
n-1+1)+N(2
n-1+2)+…+N(2
n-1)
=1+3+5+…+2
n-1=
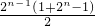
=4
n-1.
当n=3时,S(3)=16.
故答案为:16;4
n-1.
分析:由题意当n∈N
*时,定义函数N(n)表示n的最大奇因数,利用此定义有知道N(2
n)=1,当n为奇数时,N(n)=n,在从2
n-1到2
n-1这2
n-1个数中,奇数和偶数各有2
n-2个.且在这2
n-2个偶数中,不同的偶数的最大奇因数一定不同,那么N(2
n-1)+N(2
n-1+1)+N(2
n-1+2)+…+N(2
n-1),利用累加法即可求得.
点评:此题重点考查了学生对于新定义的准确理解,另外找准要求的和式具体的数据,有观察分析要求的和式的特点选择累加求和,并计算中需用等比数列的求和公式,重点是了学生的理解能力及计算能力.

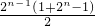 =4n-1.
=4n-1.
