
分析 可判断x=1是函数F(x)的零点,0不是方程|x2-1|-k(x2-x)+2(x-1)=0的根,从而可得k=$\frac{|{x}^{2}-1|+2(x-1)}{x(x-1)}$=$\left\{\begin{array}{l}{\frac{|x+1|+2}{x},x>1}\\{\frac{-|x+1|+2}{x},x<1且x≠0}\end{array}\right.$,从而作图求解.
解答 解:函数F(x)=f(x)-g(x)
=|x2-1|-(kx2-(2+k)x+2)
=|x2-1|-k(x2-x)+2(x-1),
故x=1是函数F(x)的零点,
故函数F(x)=f(x)-g(x)有且只有一个不是1的零点,
显然0不是方程|x2-1|-k(x2-x)+2(x-1)=0的根,
∴|x2-1|-k(x2-x)+2(x-1)=0,
∴k=$\frac{|{x}^{2}-1|+2(x-1)}{x(x-1)}$=$\left\{\begin{array}{l}{\frac{|x+1|+2}{x},x>1}\\{\frac{-|x+1|+2}{x},x<1且x≠0}\end{array}\right.$,
作函数h(x)=$\left\{\begin{array}{l}{\frac{|x+1|+2}{x},x>1}\\{\frac{-|x+1|+2}{x},x<1且x≠0}\end{array}\right.$的图象如下,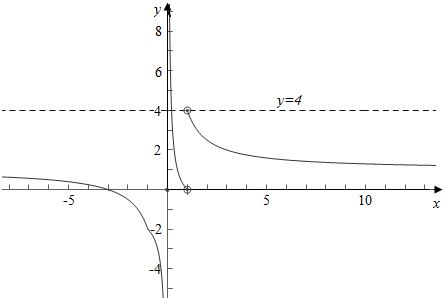 ,
,
结合图象可知,实数k的取值范围是(-∞,0]∪[4,+∞).
故答案为:(-∞,0]∪[4,+∞).
点评 本题考查了数形结合的思想应用及分类讨论的思想应用.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:填空题
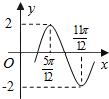 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数表达式为y=2sin(2x-$\frac{π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数表达式为y=2sin(2x-$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2-$\frac{\sqrt{2}}{2}$,2+$\frac{\sqrt{2}}{2}$] | B. | [$\frac{11}{4}$-$\frac{3\sqrt{2}}{2}$,2-$\frac{\sqrt{2}}{2}$] | C. | [2+$\frac{\sqrt{2}}{2}$,$\frac{11}{4}$+$\frac{3\sqrt{2}}{2}$] | D. | [$\frac{11}{4}$-$\frac{3\sqrt{2}}{2}$,$\frac{11}{4}$+$\frac{3\sqrt{2}}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x与y=$\sqrt{{x}^{2}}$ | B. | y=$\sqrt{{x}^{2}}$与y=($\sqrt{x}$)2 | ||
| C. | y=x+1与y=$\frac{{x}^{2}-1}{x-1}$ | D. | f(x)=x2-1与g(t)=t2-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com