Question

已知圆柱的体积为2π，则圆柱表面积的最小值为     ．

Answer 1

【答案】分析：本题考查的是圆柱的表面积和体积问题．在解答时，首先要根据题意列出表面积关于圆柱中某个量的目标函数，充分利用所给的条件减少自变量并研究自变量的取值范围．最终根据目标函数求最值即可获得问题的解答．
解答：解：由题意可知：设圆柱的底面半径为r，母线长为l，体积为V，表面积为S．
则：V=2π，π•r²•l=V，
∴，
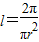
所以圆柱的表面积为：
=

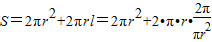
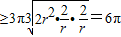
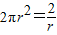
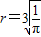
当且仅当时，即时等号成立．
故答案为：6π．
点评：本题考查的是圆柱的表面积和体积问题．在解答问题的过程当中充分体现了目标函数的思想、问题转化的思想以及函数求最值的思想．值得同学们体会反思．