
宇宙深处有一颗美丽的行星,这个行星是一个半径为r(r>0)的球。人们在行星表面建立了与地球表面同样的经纬度系统。已知行星表面上的A点落在北纬60°,东经30°;B点落在东经30°的赤道上;C点落在北纬60°,东经90°。在赤道上有点P满足PB两点间的球面距离等于AB两点间的球面距离。
(1)求AC两点间的球面距离;
(2)求P点的经度;
(3)求AP两点间的球面距离。
【解析】
试题分析:(1)根据纬度、经度的定义求出 的长,在由余弦定理求
的长,在由余弦定理求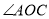 的大小,然后用弧长公式
的大小,然后用弧长公式
求AC两点间的球面距离,(2)由球面距离定义知∠POB=∠AOB=60°,又P点在赤道上,根据经度的定义可确定P点的经度;(3)连接 A,
A, C,
C,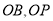 ,可知
,可知 A平行OB且等于OB的一半,延长BA与
A平行OB且等于OB的一半,延长BA与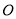
 交于D点,那么
交于D点,那么 ,同理可证
,同理可证 ,即四边形
,即四边形 为等腰梯形,求出
为等腰梯形,求出 的长,然后解三角形
的长,然后解三角形 可得
可得 的大小。
的大小。
试题解析:设球心为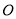 ,北纬60°圈所对应的圆心为
,北纬60°圈所对应的圆心为 ,
,
(1)那么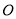
 =
=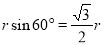 。
。 A=
A= C=
C=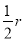 。又因为∠A
。又因为∠A C=60°。
C=60°。
所以AC=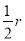 。那么由余弦定理得
。那么由余弦定理得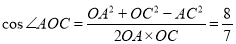
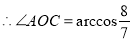 ,则AC两点间的球面距离为
,则AC两点间的球面距离为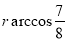 。
。
(2)PB两点间的球面距离等于AB两点间的球面距离,所以PB=AB。
可知∠POB=∠AOB=60°,又P点在赤道上,所以P点的经度为东经90°或西经30°。
显然P点的两种可能对应的AP间的球面距离相等。不妨P所在的经度为东经90°。
由条件可知 A平行OB且等于OB的一半,延长BA与
A平行OB且等于OB的一半,延长BA与
 交于D点,那么
交于D点,那么 。
。
而 C平行OP且等于OP的一半,所以D、P、C共线且
C平行OP且等于OP的一半,所以D、P、C共线且 。
。
可知AC∥BP,所以A、B、C、P共面。
又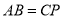 ,所以四边形
,所以四边形 为等腰梯形,
为等腰梯形,
所以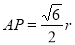 ,
,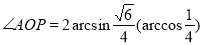 ,
,
所以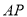 两点之间的球面距离为
两点之间的球面距离为
考点:(1)纬(经)的定义;(2)球面距离的定义与求法;(3)余弦定理的应用;(4)反三角函数的应用。


科目:高中数学 来源:2015届上海市高二4月阶段测试数学试卷(解析版) 题型:填空题
已知椭圆 (
( )的两个焦点为
)的两个焦点为 ,以
,以 为边作正三角形,若椭圆恰好平分正三角形的另外两条边,且
为边作正三角形,若椭圆恰好平分正三角形的另外两条边,且 ,则
,则 等于___________.
等于___________. (
( 不扣分)
不扣分)
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科预测二(解析版) 题型:选择题
点( )满足条件x2+y2≤4,若直线y=x+2与圆x2+y2=4相交于A、B两点,则点(
)满足条件x2+y2≤4,若直线y=x+2与圆x2+y2=4相交于A、B两点,则点( )在∆AOB(O为坐标原点)内的概率为( )
)在∆AOB(O为坐标原点)内的概率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科预测一(解析版) 题型:选择题
若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(3)-f(4)=( )
A.-1 B.1 C.-2 D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com