
 如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F恰好是抛物线y2=2px(p>0)的焦点,且两曲线的公共点连线AB过F,则双曲线的离心率是$\sqrt{2}$+1.
如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F恰好是抛物线y2=2px(p>0)的焦点,且两曲线的公共点连线AB过F,则双曲线的离心率是$\sqrt{2}$+1. 分析 先根据抛物线方程得到焦点坐标和交点坐标,代入双曲线,把$\frac{p}{2}$=c代入整理得c4-6a2c2+a4=0等式两边同除以a4,得到关于离心率e的方程,进而可求得e.
解答 解:由题意,∵两条曲线交点的连线过点F
∴两条曲线交点为($\frac{p}{2}$,p),即(c,p)
代入双曲线方程得化简得 c4-6a2c2+a4=0
∴e4-6e2+1=0
∴e2=3+2$\sqrt{2}$=(1+$\sqrt{2}$)2
∴e=$\sqrt{2}$+1
故答案为$\sqrt{2}$+1.
点评 本题考查由圆锥曲线的方程求焦点、考查双曲线的三参数的关系:c2=a2+b2注意与椭圆的区别.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 患心脏病 | 患其它病 | 总计 | |
| 秃顶 | 214 | 175 | 389 |
| 不秃顶 | 451 | 597 | 1048 |
| 总计 | 665 | 772 | 1437 |
| A. | 秃顶与患心脏病一定有关系 | |
| B. | 在犯错误的概率不超过0.010的前提下,认为秃顶与患心脏病有关系 | |
| C. | 我们有1%的把握认为秃顶与患心脏病有关系 | |
| D. | 在犯错误的概率不超过0.010的前提下,认为秃顶与患心脏病没有关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{b}$=(1,0,0),$\overrightarrow{n}$=(-2,0,0) | B. | $\overrightarrow{b}$=(1,3,5),$\overrightarrow{n}$=(1,0,1) | ||
| C. | $\overrightarrow{b}$=(0,2,1),$\overrightarrow{n}$=(-1,0,-1) | D. | $\overrightarrow{b}$=(1,-1,3),$\overrightarrow{n}$=(0,3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
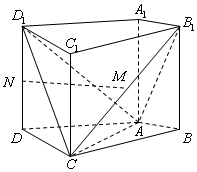 如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=3,AC=AA1=6,AD=CD=5,且点M和N分别为B1C和D1D的中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=3,AC=AA1=6,AD=CD=5,且点M和N分别为B1C和D1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-3y=0 | B. | x+y+5=0 | ||
| C. | 2x-3y=0或x+y+5=0 | D. | x+y+5=0或x-y+1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com