
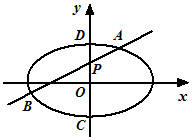
 ��ͼ����ԲE��$\frac{x^2}{4}+\frac{y^2}{b^2}=1��0��b��2��$����P��0��1���ڶ���CD�ϣ���$\overrightarrow{PC}•\overrightarrow{PD}=-2$
��ͼ����ԲE��$\frac{x^2}{4}+\frac{y^2}{b^2}=1��0��b��2��$����P��0��1���ڶ���CD�ϣ���$\overrightarrow{PC}•\overrightarrow{PD}=-2$���� ��������֪�ɵõ�C��D������ֱ�Ϊ��0��-b������0��b�������$\overrightarrow{PC}$•$\overrightarrow{PD}$=-2��ʽ���b������Բ���̿���һ�����c�ɵ���Բ�������ʣ�
����ֱ��AB��б�ʴ���ʱ����ֱ��AB�ķ���Ϊy=kx+1��A��B������ֱ�Ϊ��x1��y1������x2��y2��������ֱ�߷��̺���Բ���̣����ø���ϵ���Ĺ�ϵ�ɵ�A��B������ĺ����$\overrightarrow{OA}$•$\overrightarrow{OB}$+��$\overrightarrow{PA}$•$\overrightarrow{PB}$����֪����=2ʱ��$\overrightarrow{OA}$•$\overrightarrow{OB}$+��$\overrightarrow{PA}$•$\overrightarrow{PB}$=-7Ϊ��ֵ����ֱ��ABб�ʲ�����ʱ��ֱ��AB��Ϊֱ��CD������$\overrightarrow{OA}$•$\overrightarrow{OB}$+��$\overrightarrow{PA}$•$\overrightarrow{PB}$=$\overrightarrow{OC}$•$\overrightarrow{OD}$+2$\overrightarrow{PC}$•$\overrightarrow{PD}$=-3-4=-7���ʴ��ڳ�����=2��ʹ��$\overrightarrow{OA}$•$\overrightarrow{OB}$+��$\overrightarrow{PA}$•$\overrightarrow{PB}$Ϊ��ֵ-7��
��� �⣺��������֪����C��D������ֱ�Ϊ��0��-b������0��b����
�ֵ�P������Ϊ��0��1������$\overrightarrow{PC}$•$\overrightarrow{PD}$=-2����1-b2=-2��
���b2=3��
����ԲE����Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$��
��c=$\sqrt{{a}^{2}-{b}^{2}}$=1����������e=$\frac{1}{2}$��
����ֱ��AB��б�ʴ���ʱ����ֱ��AB�ķ���Ϊy=kx+1��A��B������ֱ�Ϊ��x1��y1������x2��y2����
����$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}=1\\ y=kx+1\end{array}\right.$���ã�4k2+3��x2+8kx-8=0��
���б�ʽ����0��
x1+x2=$\frac{-8k}{{4{k^2}+3}}$��x1x2=$\frac{-8}{{4{k^2}+3}}$��
�Ӷ���$\overrightarrow{OA}$•$\overrightarrow{OB}$+��$\overrightarrow{PA}$•$\overrightarrow{PB}$=x1x2+y1y2+��[x1x2+��y1-1����y2-1��]
=��1+�ˣ���1+k2��x1x2+k��x1+x2��+1
=$\frac{{-8��{1+��}����{1+{k^2}}��-4{k^2}+3}}{{4{k^2}+3}}$=$\frac{4-2��}{{4{k^2}+3}}$-2��-3��
����=2ʱ��$\frac{4-2��}{{4{k^2}+3}}$-2��-3=-7��
��$\overrightarrow{OA}$•$\overrightarrow{OB}$+��$\overrightarrow{PA}$•$\overrightarrow{PB}$=-7Ϊ��ֵ��
��ֱ��ABб�ʲ�����ʱ��ֱ��AB��Ϊֱ��CD��
��ʱ$\overrightarrow{OA}$•$\overrightarrow{OB}$+��$\overrightarrow{PA}$•$\overrightarrow{PB}$=$\overrightarrow{OC}$•$\overrightarrow{OD}$+2$\overrightarrow{PC}$•$\overrightarrow{PD}$=-3-4=-7��
�ʴ��ڳ�����=2��ʹ��$\overrightarrow{OA}$•$\overrightarrow{OB}$+��$\overrightarrow{PA}$•$\overrightarrow{PB}$Ϊ��ֵ-7��
���� ���⿼����Բ�ļ����ʣ�����ֱ������Բλ�ù�ϵ��Ӧ�ã�ѵ����ƽ�����������Բ���������е�Ӧ�ã������ˡ�������Ľ���˼�뷽�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Vp��?x��[0��2��]��sinx��1 | B�� | �Vp��?x��[-2��0]��sinx��1 | ||
| C�� | �Vp��?x��[0��2��]��sinx��1 | D�� | �Vp��?x��[-2��0]��sinx��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{3}-1}}{2}$ | B�� | $\sqrt{3}-1$ | C�� | $\frac{{\sqrt{3}-\sqrt{2}}}{2}$ | D�� | $\frac{{\sqrt{3}+1}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | nxn-1e-x | B�� | xne-x | C�� | 2xne-x | D�� | ��n-x��xn-1e-x |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com