
【题目】如图,在正三棱柱![]() 中,点
中,点![]() 是棱
是棱![]() 的中点,
的中点,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,利用四边形
,利用四边形![]() 是平行四边形,进而证明出
是平行四边形,进而证明出![]() ∥
∥![]() ,即可利用线面平行的判定定理,证得
,即可利用线面平行的判定定理,证得![]() 平面
平面![]() ;(2)分别以
;(2)分别以![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,分别求解平面
轴建立空间直角坐标系,分别求解平面![]() 和平面
和平面![]() 的一个法向量,利用向量的夹角公式,即可求解二面角
的一个法向量,利用向量的夹角公式,即可求解二面角![]() 的平面角的余弦值,进而求解其正弦值.
的平面角的余弦值,进而求解其正弦值.
试题解析:(Ⅰ)证明:连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
在正三棱柱![]() 中,四边形
中,四边形![]() 是平行四边形,∴
是平行四边形,∴![]() .
.
∵![]() ,∴
,∴![]() ∥
∥![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() , ∴
, ∴![]() ∥平面
∥平面![]() .
.
(2)过点![]() 作
作![]() 交
交![]() 于
于![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() .因为平面
.因为平面![]()
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .分别以
.分别以![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,如图所示.因为
轴建立空间直角坐标系,如图所示.因为![]() ,
,![]() 是等边三角形,所以
是等边三角形,所以![]() 为
为![]() 的中点.则
的中点.则![]() ,
,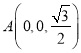 ,
,![]() ,
,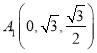 ,
,![]() ,
,![]() ,B(
,B(![]() ,0,0)
,0,0)
(Ⅰ)设平面![]() 的法向量为
的法向量为![]() ,则
,则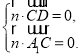
∵![]() ,
,![]() ,∴
,∴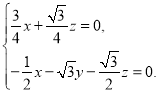
取![]() ,得平面
,得平面![]() 的一个法向量为
的一个法向量为![]()
![]() =(1,-
=(1,-![]() ,0)
,0)![]()
![]() ·
·![]() =0
=0![]() ∴
∴![]() ∥平面
∥平面![]() .
.
(Ⅱ)可求平面![]() 的一个法向量为
的一个法向量为![]() .
.
设二面角![]() 的大小为
的大小为![]() ,则
,则![]() .
.
∵![]() ,
,![]()


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC—A1B1C1中,E、F分别是A1B、A1C的中点,点D在B1C1上,A1D⊥B1C.

求证:(1)EF∥平面ABC;
(2)平面A1FD⊥平面BB1C1C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个四棱锥的三视图如图所示.

(1)求证:PA⊥BD;
(2)在线段PD上是否存在一点Q,使二面角Q-AC-D的平面角为30°?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).若直线
为参数).若直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(Ⅰ)写出圆![]() 的直角坐标方程,并求圆心的坐标与半径;
的直角坐标方程,并求圆心的坐标与半径;
(Ⅱ)若弦长![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 由归纳推理得到的结论一定正确
B. 由类比推理得到的结论一定正确
C. 由合情推理得到的结论一定正确
D. 演绎推理在前提和推理形式都正确的前提下,得到的结论一定正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列试验中,是古典概型的为( )
A.种下一粒种子,观察它是否发芽
B.从规格直径为250 mm±0.6 mm的一批合格产品中任意抽一件,测量其直径d
C.抛一枚硬币,观察其向上的面
D.某人射击中靶或不中靶
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若事件A和B是互斥事件,且P(A)=0.1,则P(B)的取值范围是( )
A. [0,0.9] B. [0.1,0.9] C. (0,0.9] D. [0,1]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com