练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     已知f(m)＝1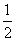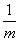＋＋＋…＋(m∈N*，m≥4)，经计算得f(4)>2，f(8)>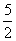，f(16)>3，f(32)>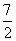，…，观察上述结果，可归纳出的一般结论为________．


    f(2n)>(n≥2，n∈N*)　

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图,O为正方体ABCDA1B1C1D1的底面ABCD的中心,则下列直线中与B1O垂直的是(　　)

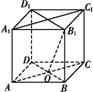
    (A)A1D (B)AA1

    (C)A1D1  (D)A1C1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    将正方形ABCD沿对角线BD折成直二面角ABDC,则下面结论错误的为(　C　)

    (A)AC⊥BD

    (B)△ACD是等边三角形

    (C)AB与平面BCD所成的角为60°

    (D)AB与CD所成的角为60°

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知圆C：x2＋(y－2)2＝5，直线l：mx－y＋1＝0.

    (1)求证：对m∈R，直线l与圆C总有两个不同的交点；

    (2)若圆C与直线l交于A，B两点，求弦AB的中点M的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列…，由此，猜想出第n个数为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用反证法证明命题“三角形的三个内角至少有一个不大于60°”时，应假设(　　)

    A．三个内角都不大于60° 

    B．三个内角都大于60°

    C．三个内角至多有一个大于60° 

    D．三个内角至多有两个大于60°

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值，则(　　)

    A．△A1B1C1和△A2B2C2都是锐角三角形 

    B．△A1B1C1和△A2B2C2都是钝角三角形

    C．△A1B1C1是钝角三角形，△A2B2C2是锐角三角形 

    D．△A1B1C1是锐角三角形，△A2B2C2是钝角三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设平面内有n条直线(n≥3)，有且仅有两条直线互相平行，任意三条直线不过同一点，若用f(n)表示平面内交点的个数，则当n≥3时，f(n)＝________．(用n表示)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知m，n是两条不同的直线，α，β，γ是三个不同的平面，下列结论中正确的有________．

    ①若m∥α，n∥α，则m∥n；

    ②若α⊥γ，β⊥γ，则α∥β；

    ③若m∥α，m∥β，则α∥β；

    ④若m⊥α，n⊥α，则m∥n.

    查看答案和解析>>

    同步练习册答案