Question

【题目】在△ABC中，∠BAC=10°，∠ACB=30°，将直线BC绕AC旋转得到B1C，直线AC绕AB旋转得到AC1 ， 则在所有旋转过程中，直线B1C与直线AC1所成角的取值范围为 ．

Answer 1

【答案】[10°，50°]
【解析】解：∵在△ABC中，∠BAC=10°，∠ACB=30°，
将直线BC绕AC旋转得到B1C，直线AC绕AB旋转得到AC1 ，
如图，平移CB1到A处，B1C绕AC旋转，
∴∠B1CA=30°，∠B1AC=150°，
AC1绕AB旋转，∴0°≤∠C1AC≤2∠CAB，
∴0≤∠C1AC≤20°，
设直线B1C与直线AC1所成角为α，
则∠B1AC﹣∠C1AC≤α≤∠B1AC+∠C1AC，
∵130°≤∠B1AC﹣∠C1AC≤150°，
150°≤∠B1AC+∠C1AC≤170°，
∴10°≤α≤50°或130°≤α≤170°（舍）．
所以答案是：[10°，50°]．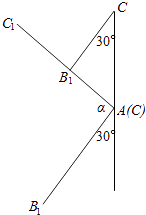

【考点精析】通过灵活运用异面直线及其所成的角，掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系即可以解答此题．