
【题目】数列{an}中,已知a1= ![]() ,an+1=
,an+1= ![]() .
.
(1)证明:an<an+1< ![]() ;
;
(2)证明:当n≥2时,( ![]() )
) ![]() <2.
<2.
【答案】
(1)证明:由 ![]() ,得
,得 ![]() ,即0≤an≤1.
,即0≤an≤1.
∴an+1= ![]() =
= ![]() ,
,
又a1= ![]() ≠0,且
≠0,且 ![]() ,∴0
,∴0 ![]() .
.
∴ ![]() >0.
>0.
即 ![]()
(2)证明:当n=2时, ![]() ,
,
又∵ ![]() ,
,
∴ ![]() .
.
即当n=2时, ![]() 成立,
成立,
当n=k时, ![]() 成立,即
成立,即 ![]() 成立,
成立,
当n=k+1时, ![]() =
= ![]() .
.
∵an+1>an,∴ak+1>ak
∴ ![]() .
.
则 ![]() =
= ![]() ,
,
∴当n=k+1时, ![]() 也成立,
也成立,
∴当n≥2时, ![]() 成立
成立
【解析】(1)由已知a1= ![]() ,an+1=
,an+1= ![]() ,即可得到
,即可得到 ![]() ,又0
,又0 ![]() ,进一步得到
,进一步得到 ![]() ,则结论an<an+1<
,则结论an<an+1< ![]() 可证;(2)首先证当n=2时,
可证;(2)首先证当n=2时, ![]() 成立,即当n=k时,
成立,即当n=k时, ![]() 成立,当n=k+1时,ak+1>ak , 则
成立,当n=k+1时,ak+1>ak , 则 ![]() =
= ![]() ,则结论当n≥2时,(
,则结论当n≥2时,( ![]() )
) ![]() <2可证.
<2可证.
【考点精析】关于本题考查的数列的通项公式,需要了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 合 计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
合 计 | 60 | 50 | 110 |
根据上述数据能得出的结论是( )
(参考公式与数据:X2= ![]() .当X2>3.841时,有95%的把握说事件A与B有关;当X2>6.635时,有99%的把握说事件A与B有关; 当X2<3.841时认为事件A与B无关.)
.当X2>3.841时,有95%的把握说事件A与B有关;当X2>6.635时,有99%的把握说事件A与B有关; 当X2<3.841时认为事件A与B无关.)
A.有99%的把握认为“爱好该项运动与性别有关”
B.有99%的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=![]() .
.
(Ⅰ)求证:AC⊥平面BEH;
(Ⅱ)求直线PA与平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,∠BAC=10°,∠ACB=30°,将直线BC绕AC旋转得到B1C,直线AC绕AB旋转得到AC1 , 则在所有旋转过程中,直线B1C与直线AC1所成角的取值范围为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A1 , A2 , …,An(n≥4)为集合S={1,2,…,n}的n个不同子集,为了表示这些子集,作n行n列的数阵,规定第i行第j列的数为: ![]() .则下列说法中,错误的是( )
.则下列说法中,错误的是( ) 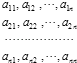
A.数阵中第一列的数全是0当且仅当A1=
B.数阵中第n列的数全是1当且仅当An=S
C.数阵中第j行的数字和表明集合Aj含有几个元素
D.数阵中所有的n2个数字之和不超过n2﹣n+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查.假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数N为( )
A.101
B.808
C.1212
D.2012
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)经过点(2,
(a>b>0)经过点(2, ![]() )且离心率等于
)且离心率等于 ![]() ,点A,B分别为椭圆C的左右顶点,点P在椭圆C上.
,点A,B分别为椭圆C的左右顶点,点P在椭圆C上.
(1)求椭圆C的方程;
(2)M,N是椭圆C上非顶点的两点,满足OM∥AP,ON∥BP,求证:三角形MON的面积是定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com